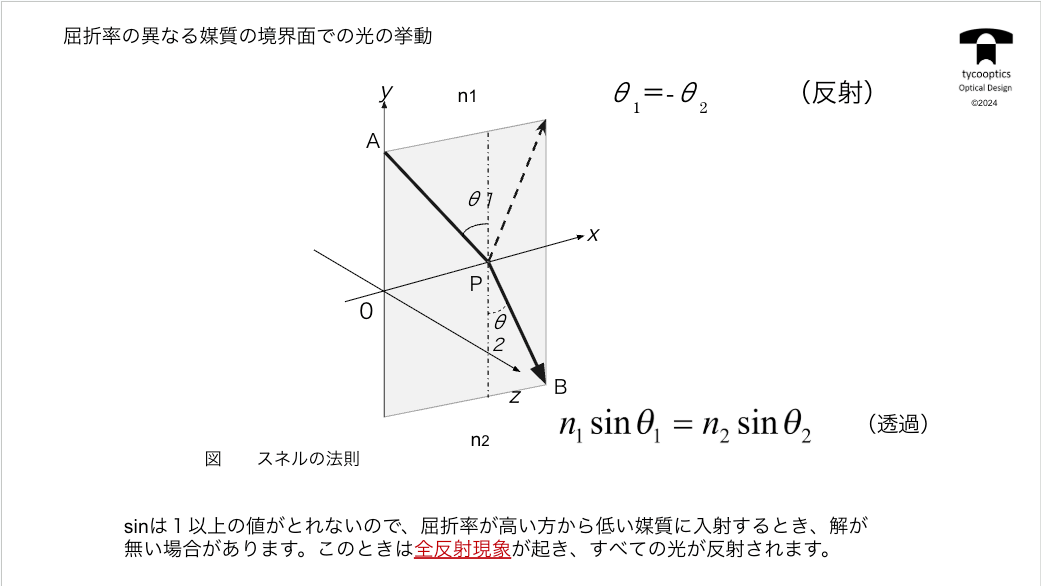
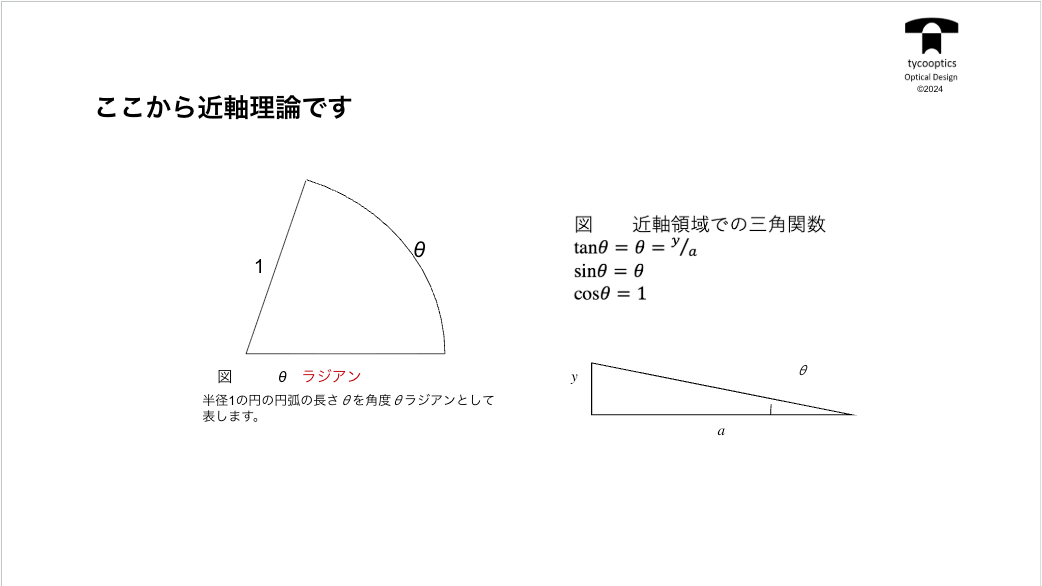
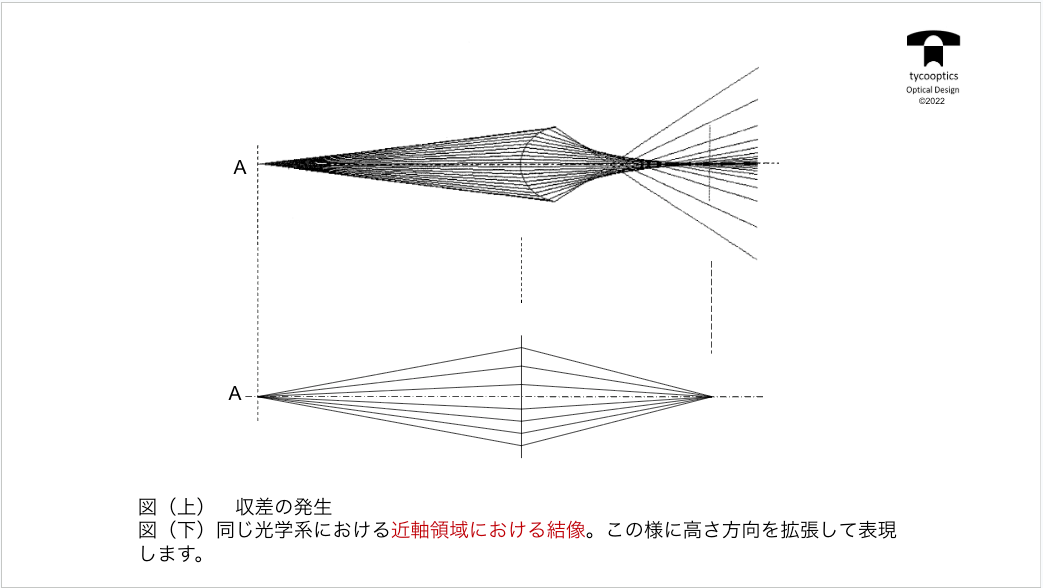
目次
- 光学設計とは:その特質と歴史
- 近軸理論:光学系の基本配置を決める
- 収差とは:色収差、球面収差、コマ収差、正弦条件
- 収差とは:像面湾曲、非点収差、歪曲収差、射影関係
- 収差の表現の仕方:レンズの性質を知る上で重要な種々の図の読みとり方
- 収差・性能を良くするための幾つかの理論、戦略、定番のレンズタイプ
- 波動光学的結像理論:レーザー光学系の設計について
- 波動光学的結像理論:レーザー光学系の設計について
- 結像性能評価MTFと像の明るさについて:Fナンバー、周辺光量
- 照明系光学設計について
- 照明系光学設計について part2
- 光学系の製造:公差/ゴースト/温度特性/光学設計の未来
光学設計とは : その特質と歴史
【照明系】
顕微鏡の照明、車の照明の構造を例に用い、照明系についてお話していきます。
【結象とは何か】
結像って何だろうということをご説明させていただきます。結像とはどういう現象を言うのかというと、例えば、文字があって、これをフィルムあるいはCCD状に再び撮る時として表現したい、あるいは取り込みたいというのは結像の要求ということになります。
【必要とされる光学理論、幾何学・波動光学】
いろんなものにも本当に使われてるということで、まず大事なことは、光学設計者は今まではカメラ会社や、電機会社の一部しかいませんでしたが、今はどんな事業にも必要なってきています。
【円形開口の回折像振幅分布】
バーチャルラボっていう、過去にコンサルやってたドイツ製のソフト、今もかなり有力なソフトと思いますけど、これで非常に面白いシミュレーションができました。どういうものかお話していきます。
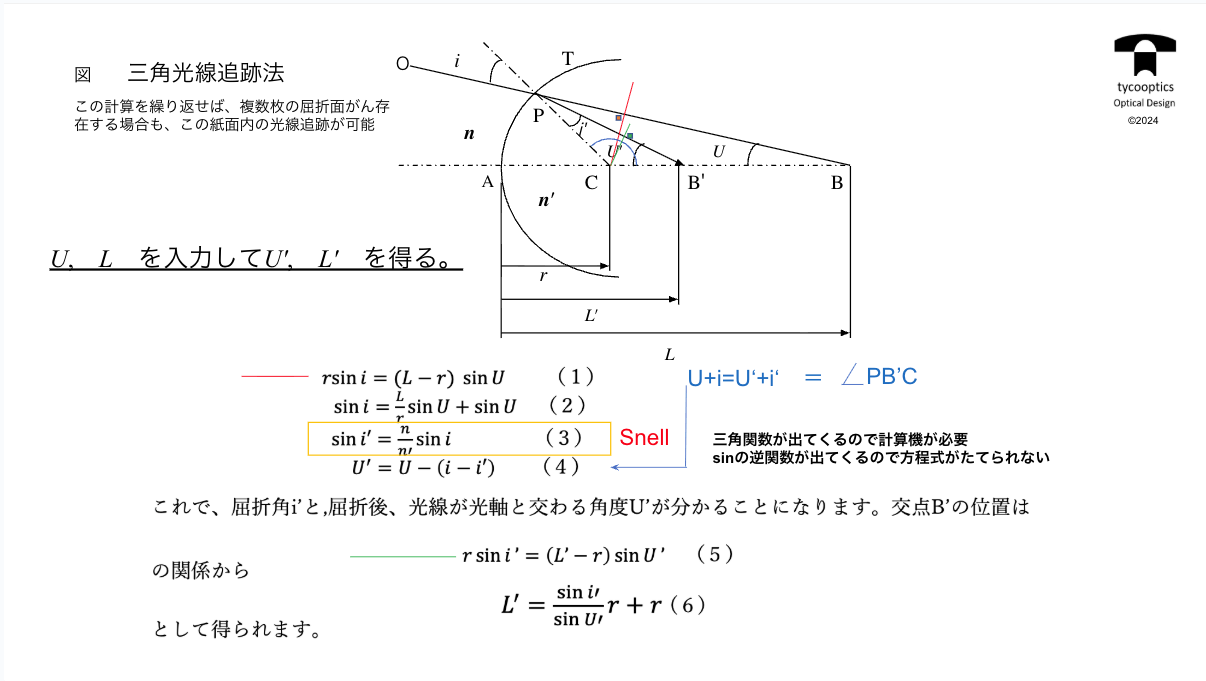
【三角光線追跡法】
三角光線追跡法についてご説明します。光線追跡技術の式、これ見ていただければ非常に簡単です。
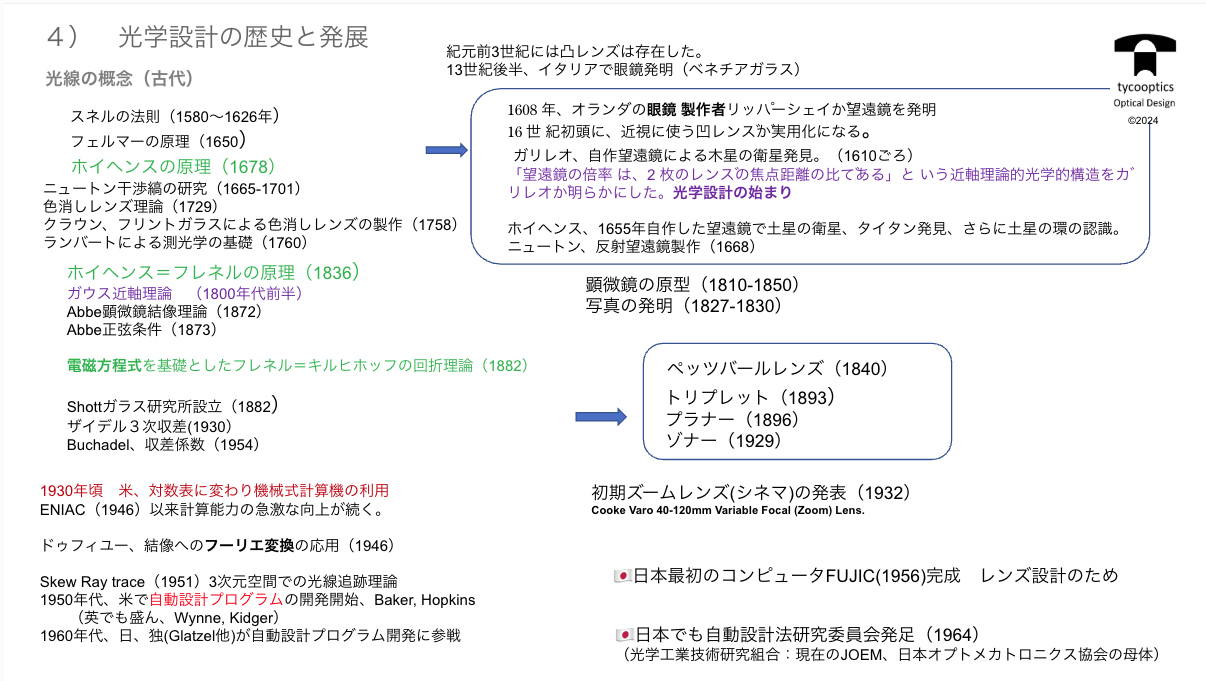
【光学設計の歴史と発展】
光学設計の歴史をまとめたものをお話します。今までの話と総合していただくとよくわかると思います。
【PCによる光学設計プログラムの機能変遷】
私が1980年ぐらいに会社に入った時には汎用コンピューターは、学校の教室1個分ぐらいあるようなコンピューターで計算してたんですけども、次々といいコンピューターが出てきて、大体1980年ぐらいからパソコンで設計できるようになりました。
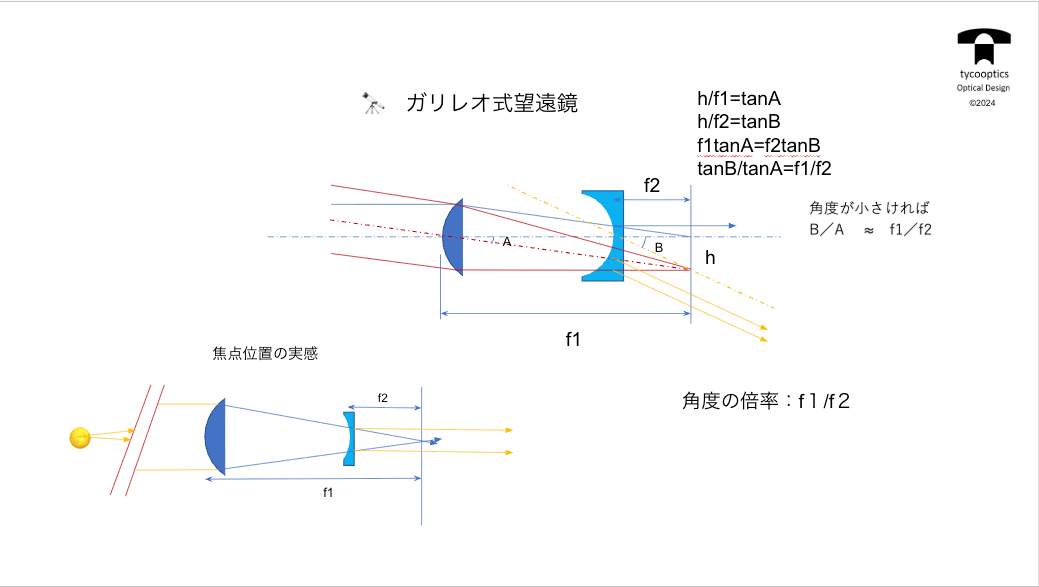
近軸理論:光学系の基本配置を決める
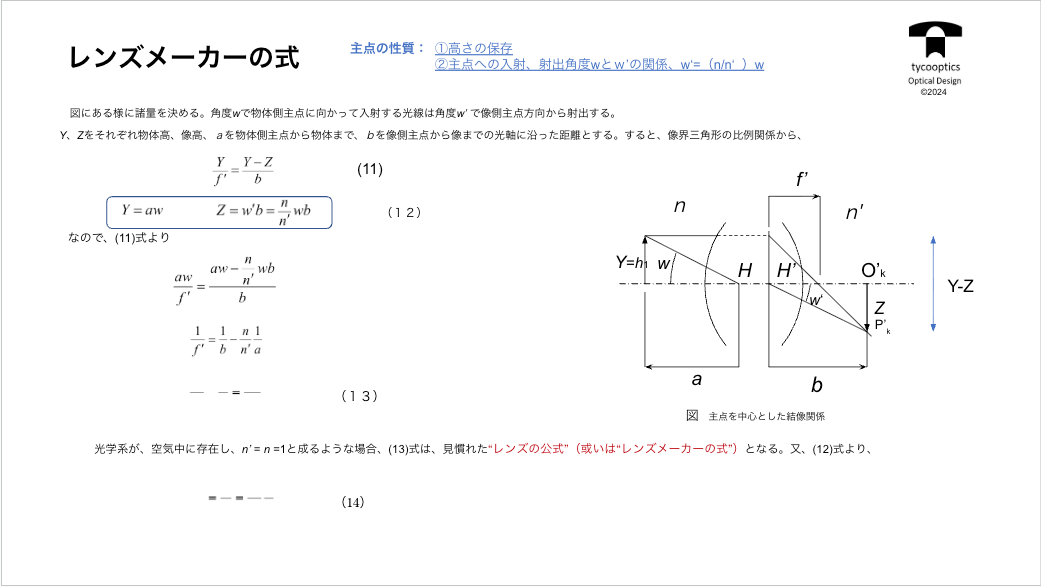
【近軸理論による結像方程式】
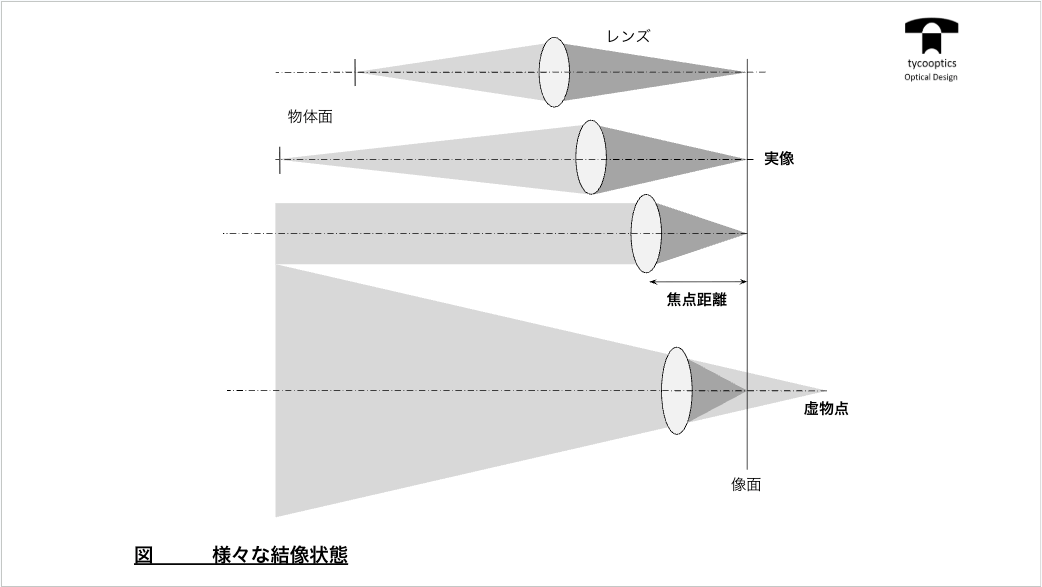
近軸理論による結像方程式について説明していきます。すごく簡単な式になるっていうのはお分かりになっていただけると思います。
【主点位置とバックフォーカス】
焦点距離が同じである。とても自由な構成ができる。ある程度の自由度がある場合に、一番最後のレンズから焦点までの距離をバックフォーカスといいます。
【倍率の概念と主点の性質】
倍率の概念と主点の性質について詳しくお話していきます。
収差とは:色収差、球面収差、コマ収差、正弦条件
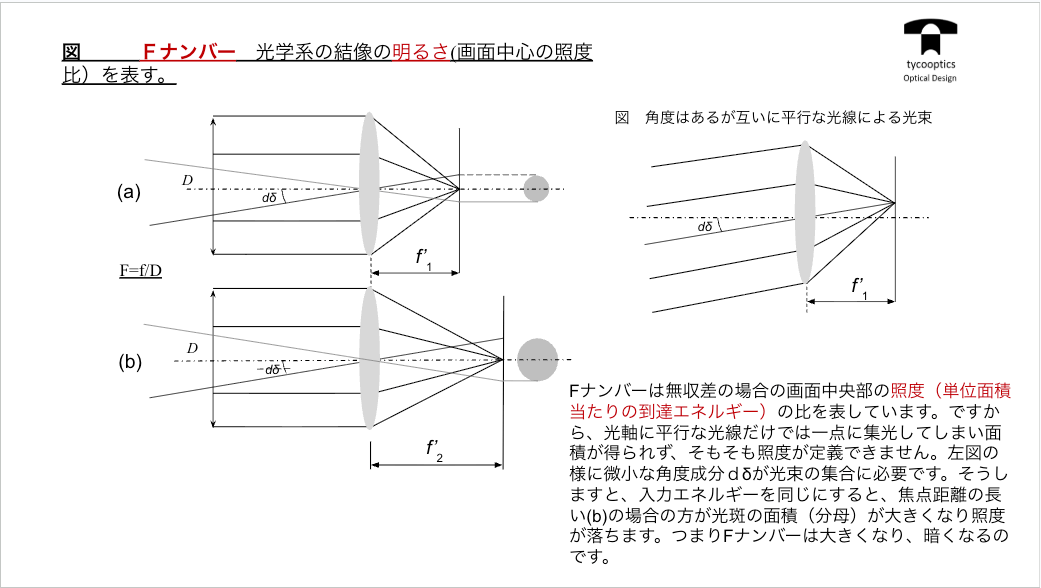
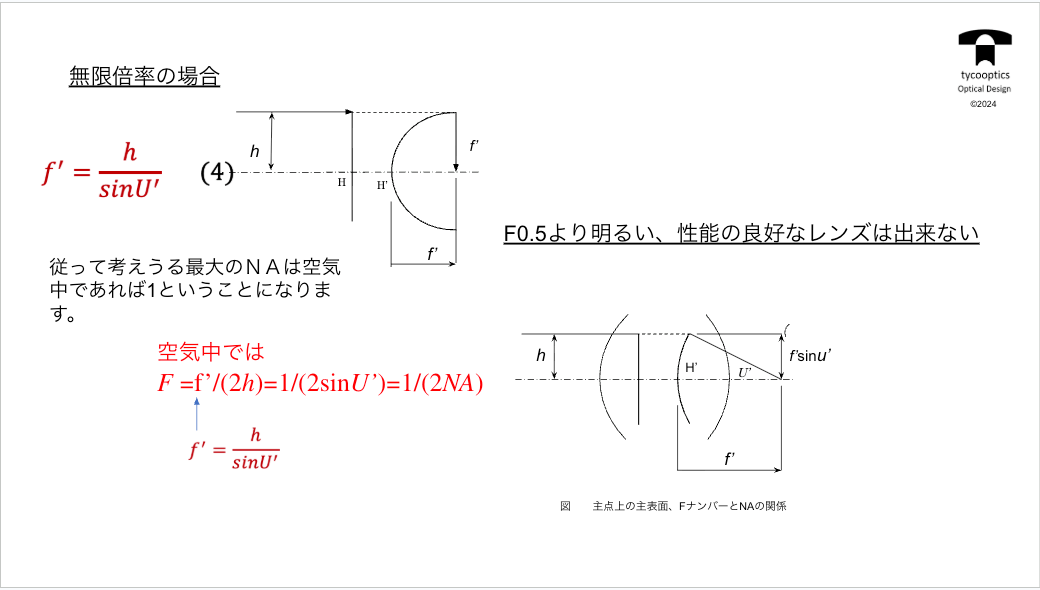
【Fナンバーと焦点距離の関係】
Fナンバーと焦点距離の関係に付いてお話していきます。このFナンバーって結局照度を表してます。画面中心付近の照度を表してます。
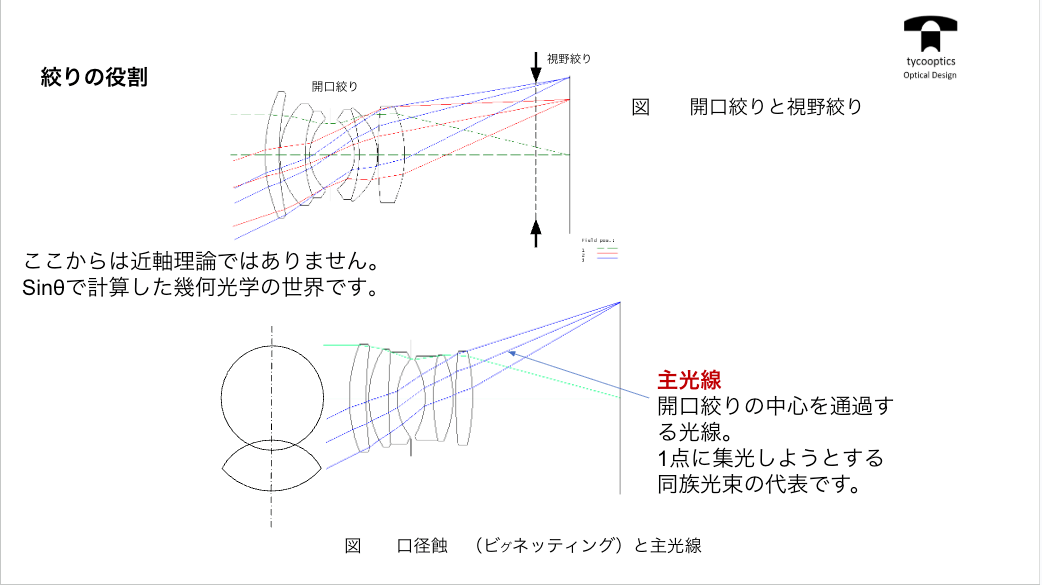
【復習】
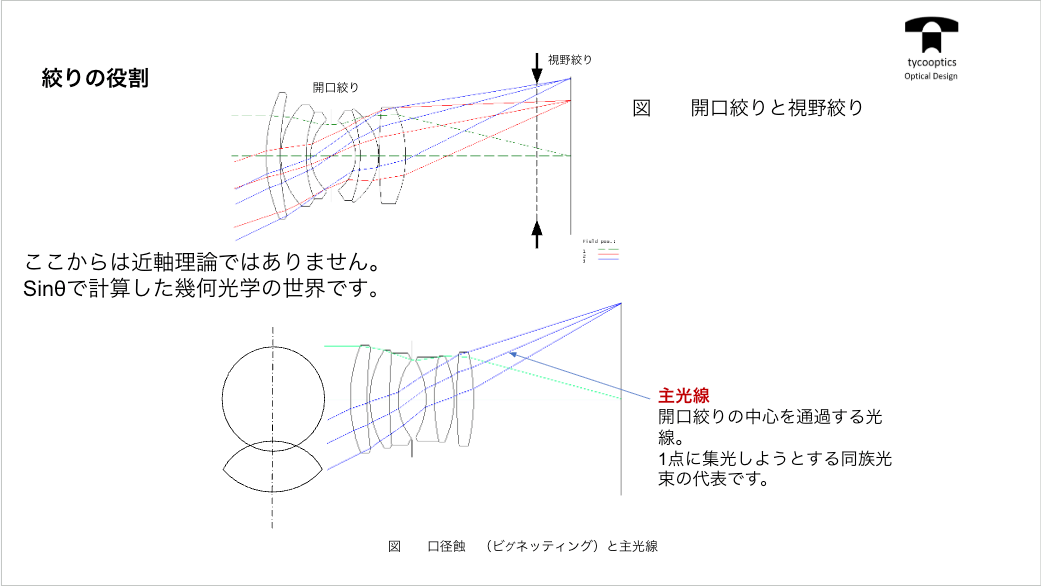
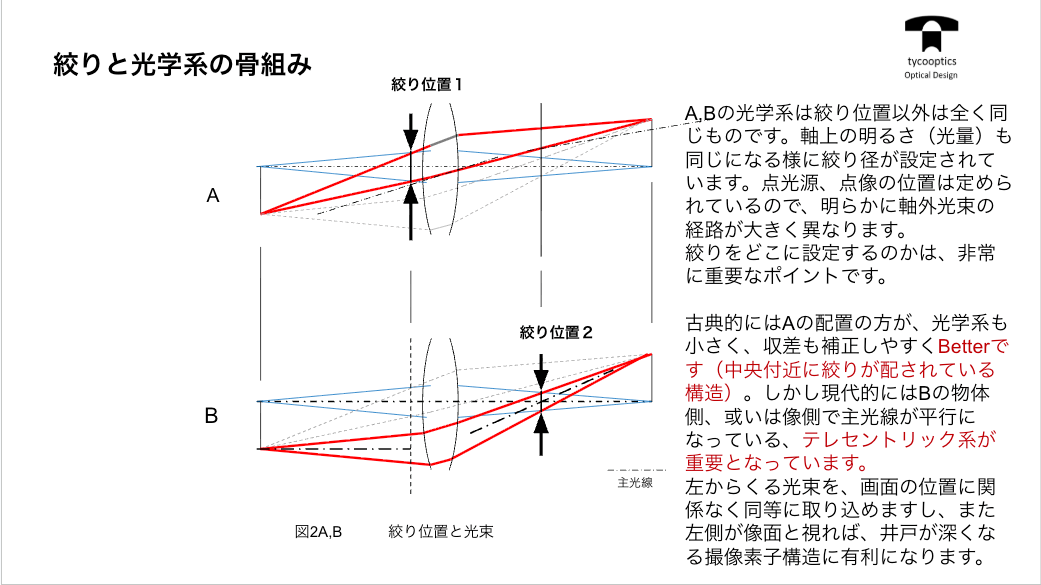
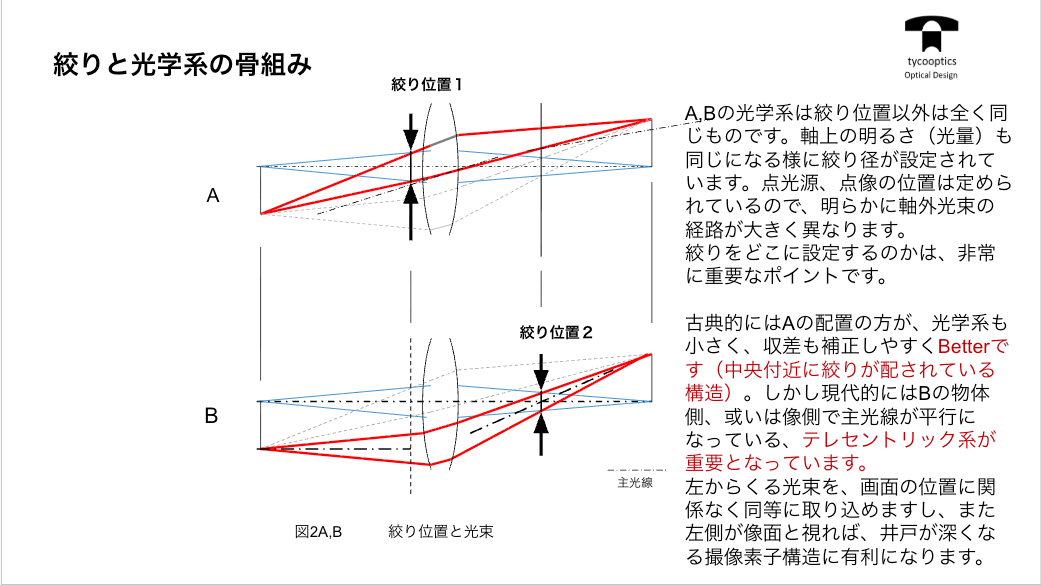
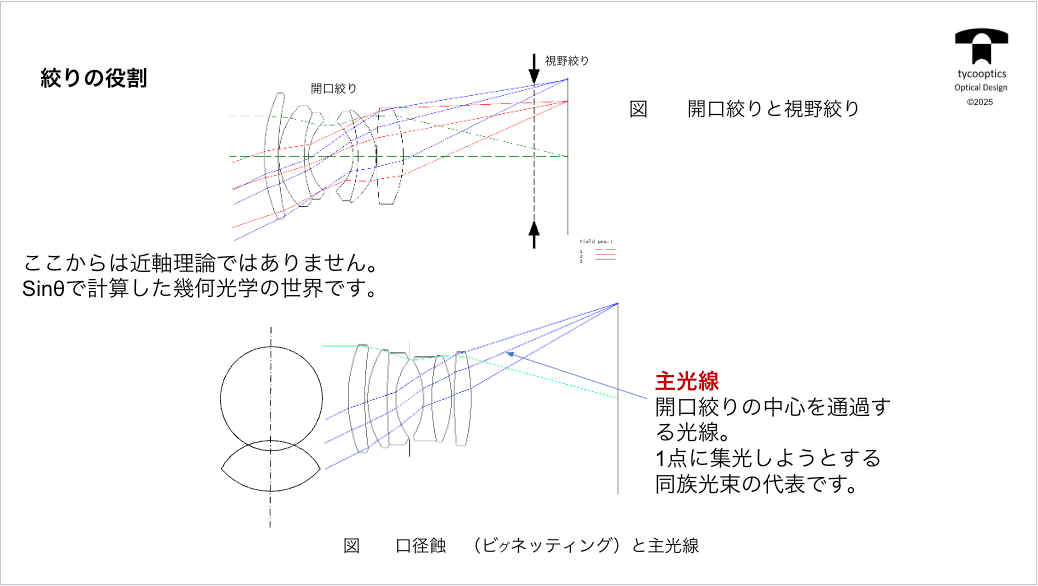
前回の積み残し分で、ちょっと復習となりますが非常にこの絞りをどこに付けるかっていうのは、実は我々工学設計者にとっては非常に重要な仕事の一つです。
【色収差とは】
ここからは、いよいよ収差とは何かということにいきます。ここまでお話しさせたいただいた近未来理論というのは、収差はなかったのです。それで光線追跡をやってみると全部1点に収束してしまうということがわかりました。
【色消しの理論】
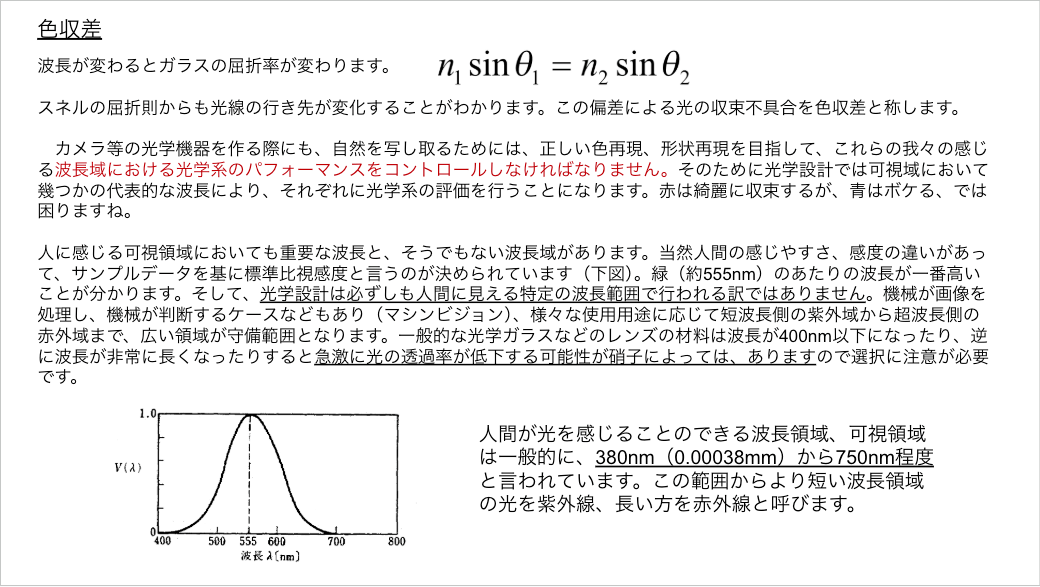
一般の教科書に出てくるのは、色というと人間の目はどのあたりまで見えるのかということです。大体380-750ナノです。これを可視域といいます。ここをふまえて話をしていきます。
【アッべ数を使用した式】
色収差についてアッペ数を使用した式でお話していきます。
【セルマイヤーの分散式】
色収差についてセルマイヤーの分散式を用いてお話していきます。
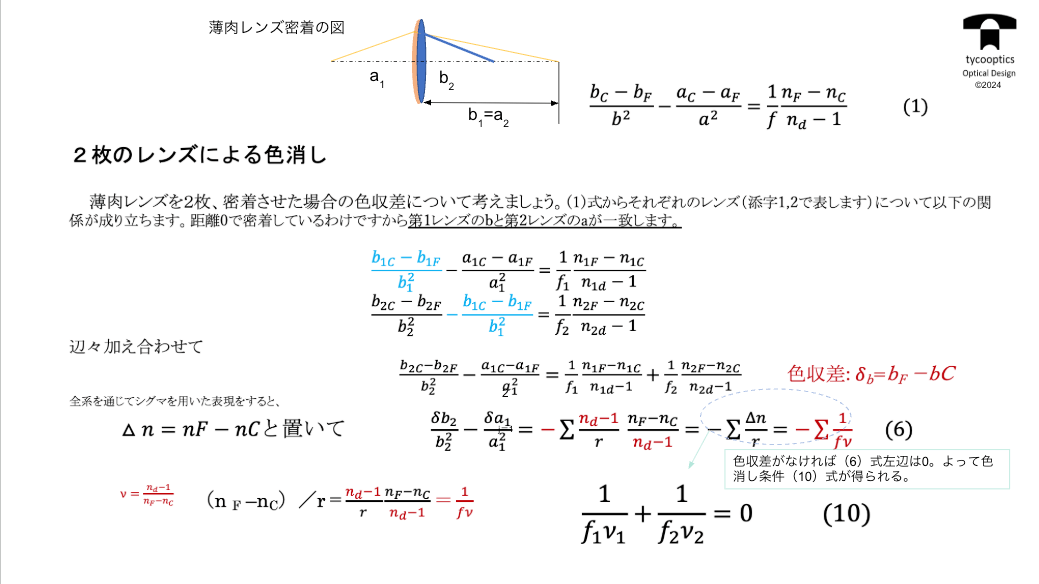
【ダブレットレンズの焦点距離の色消し条件】
ダブレットレンズの焦点距離の色消し条件をお話していきます。
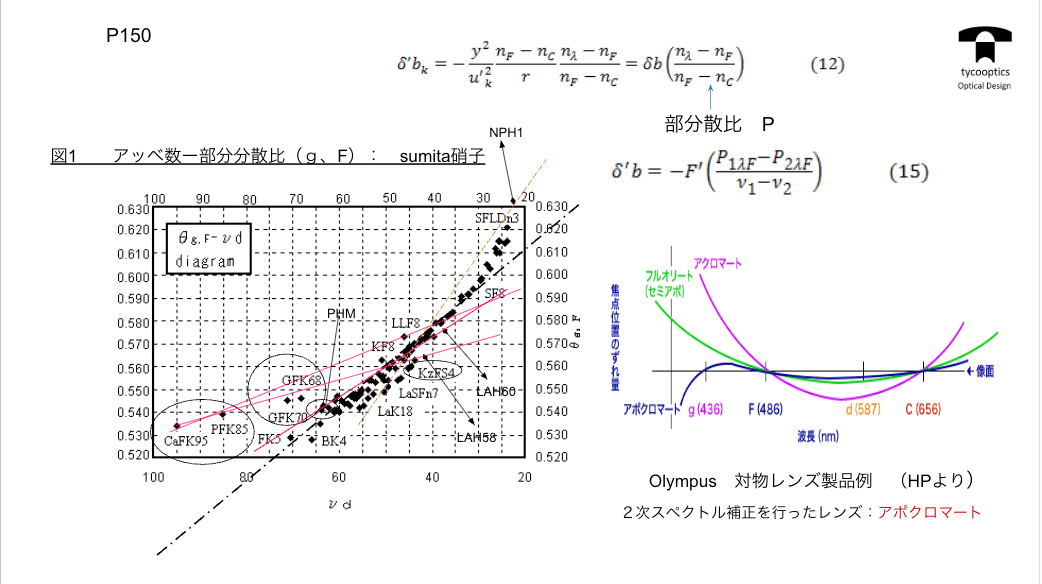
【2次スペクトルの除去】
大きい収差が発生すると、2次スペクトルを除去しないといけません。例えば望遠レンズなんか非常に大きな収差として見えてしまうということです。
【三角柱状のプリズムの断面図】
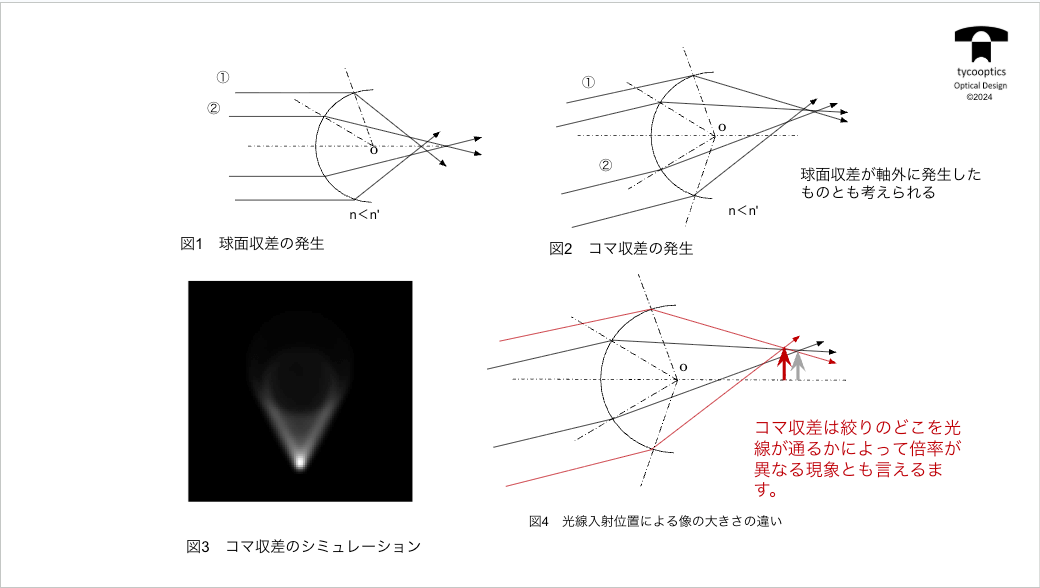
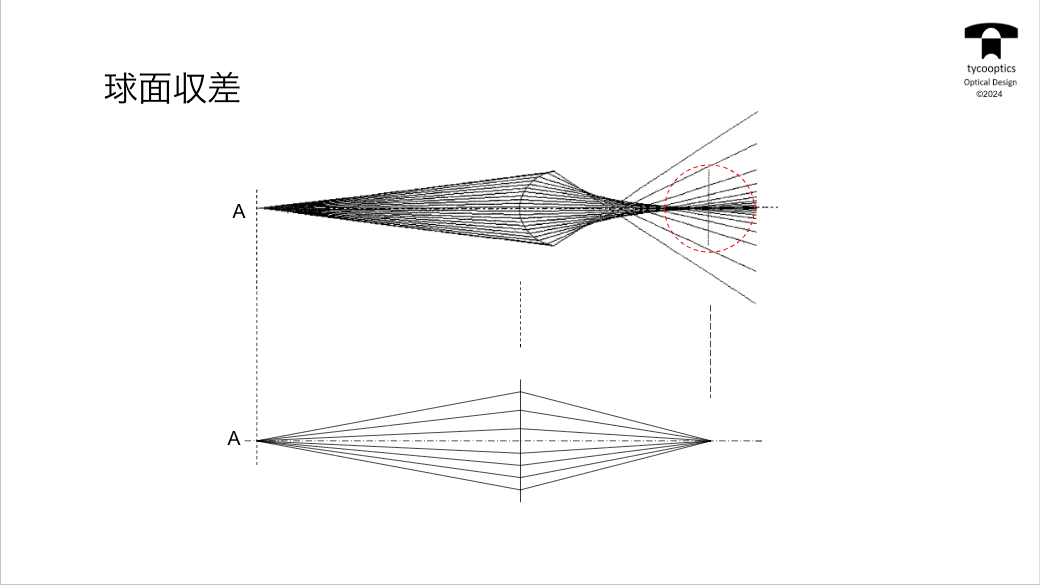
次は球面収差ですね。これはもう近未来理論ではないんですね。
【球面収差発生の図解】
そもそも球面収差って何で発生するのかな?ということなんですけど、これはよく言われてる説明があります。
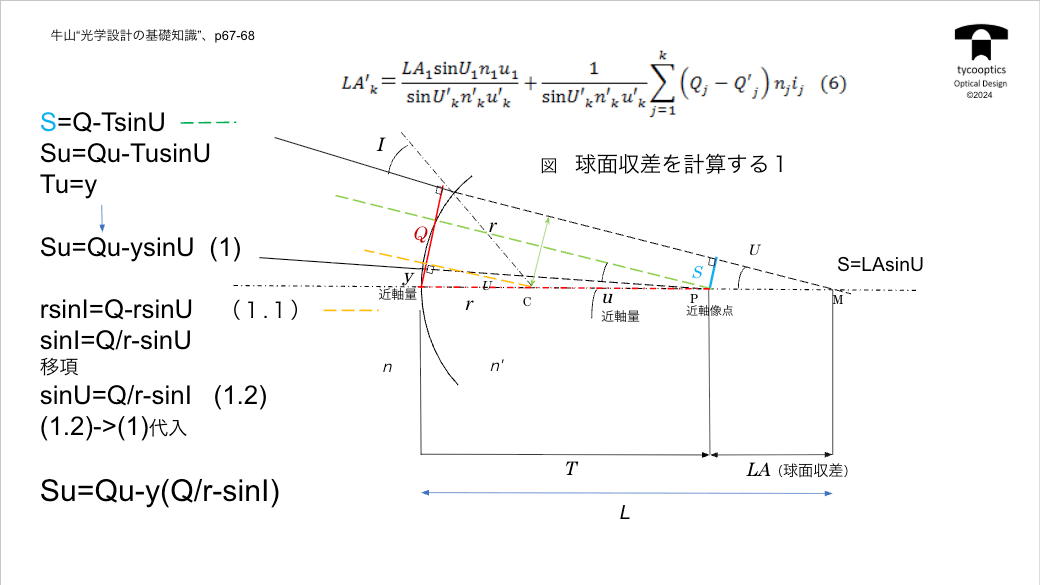
【球面収差を計算する】
これはイギリスのインペリアルカレッジの混乱っていう人による理論が元になっています。
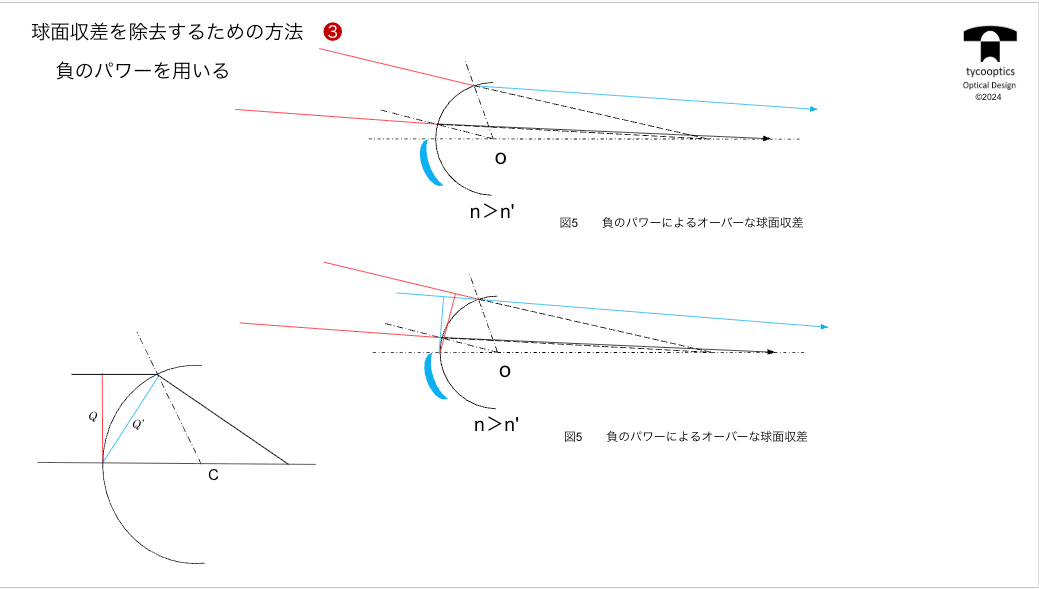
【パワーの分割の利点】
ここが重要な結論です。QとQ’の差が球面収差の直接の原因になっているですね。
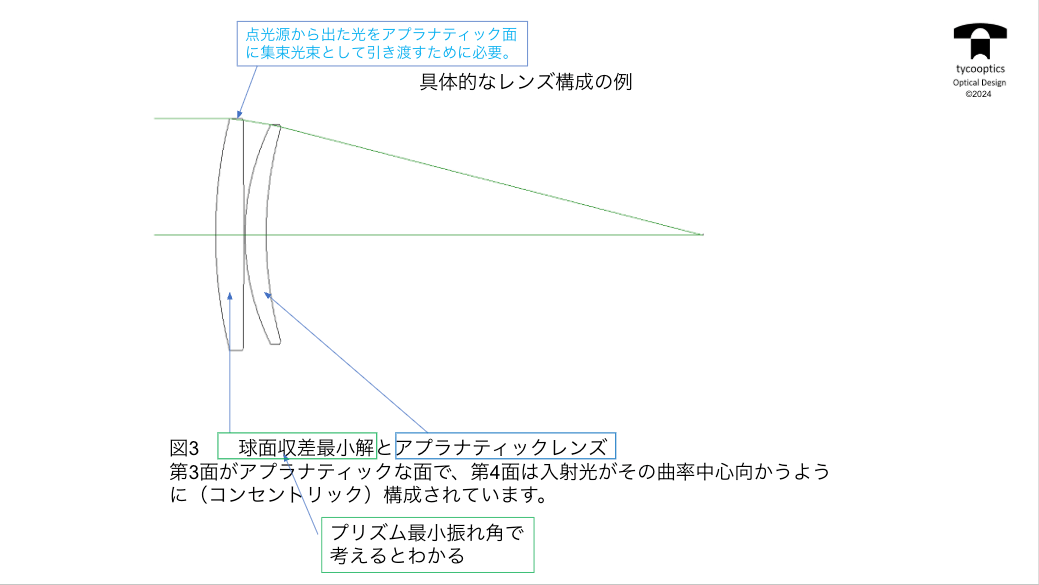
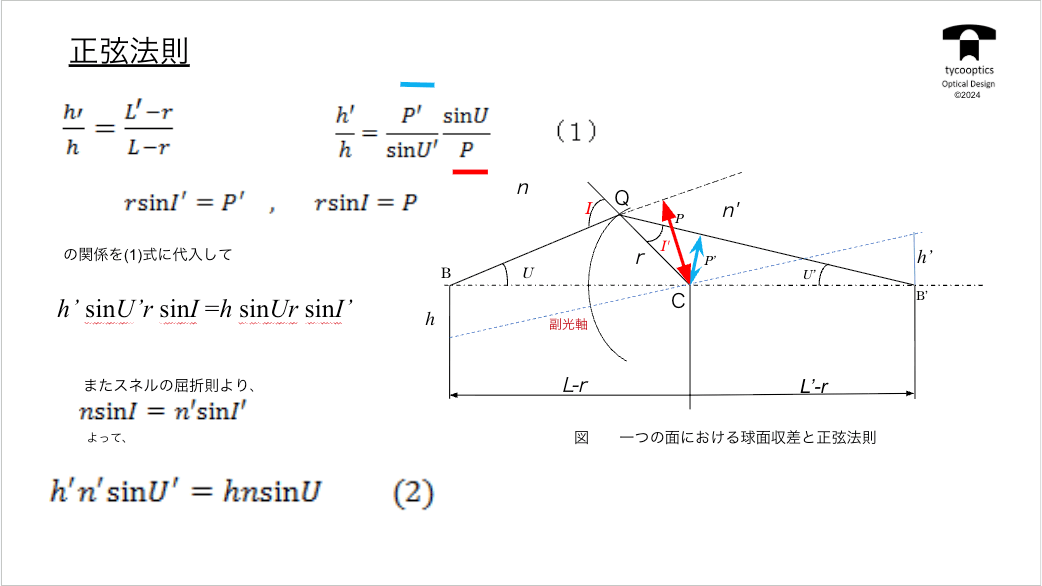
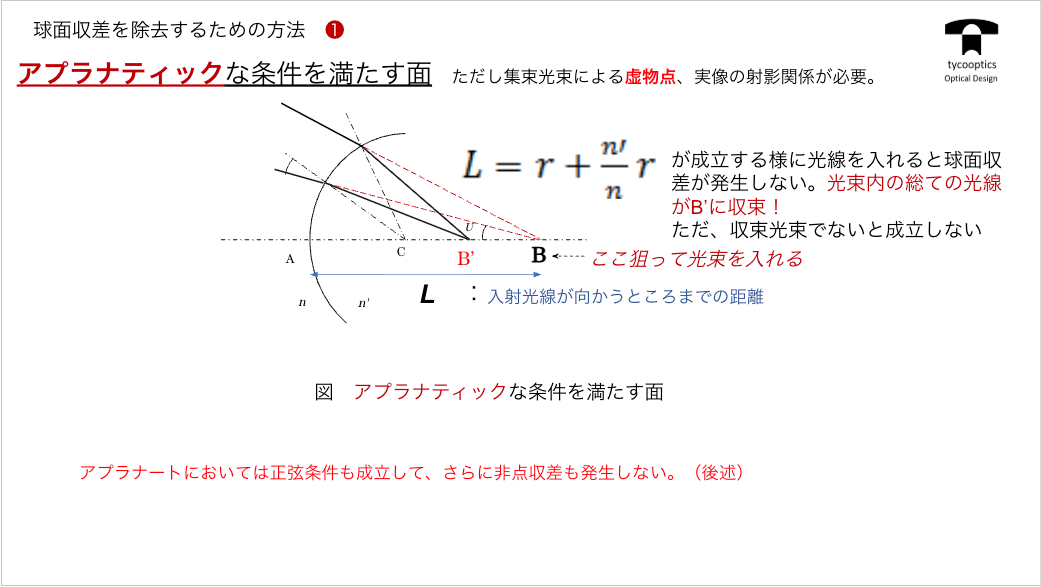
【アプラナティックな条件を満たす面】
アプラナティックな条件を満たす面についてご説明してまいります。
【球面収差とアプラナティックレンズ】
球面収差とアプラナティックレンズについてお話します。
【質疑応答】
レンズメーカの公式がメーカによって異なると伺いましたが理由は何でしょうか?
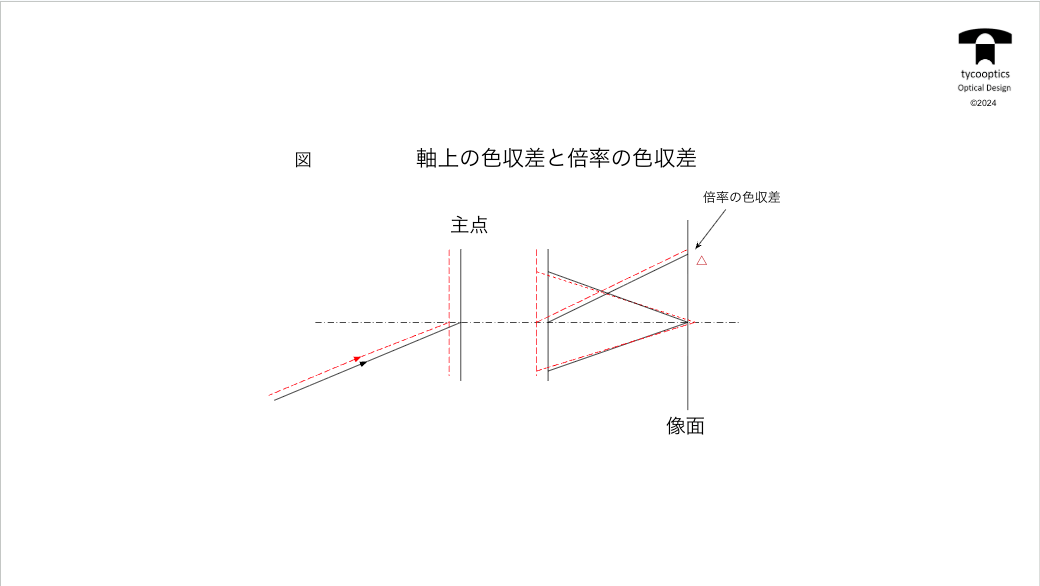
収差とは:像面湾曲、非点収差、歪曲収差、射影関係
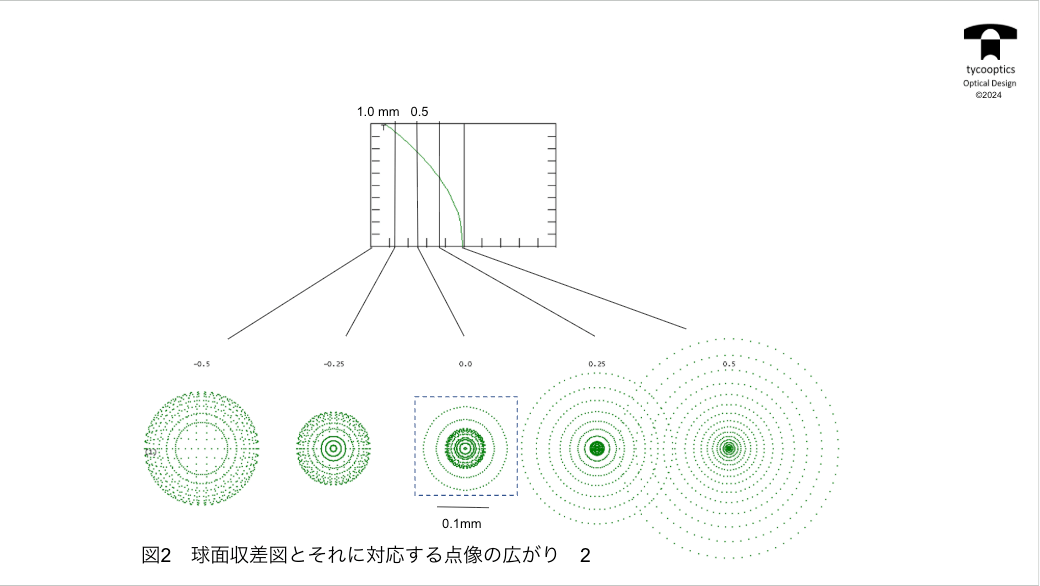
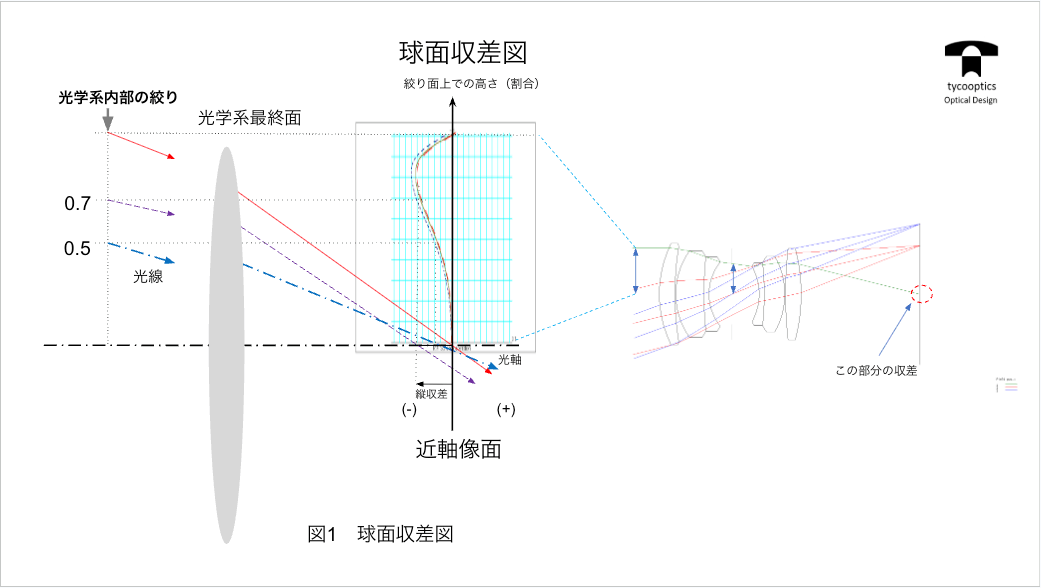
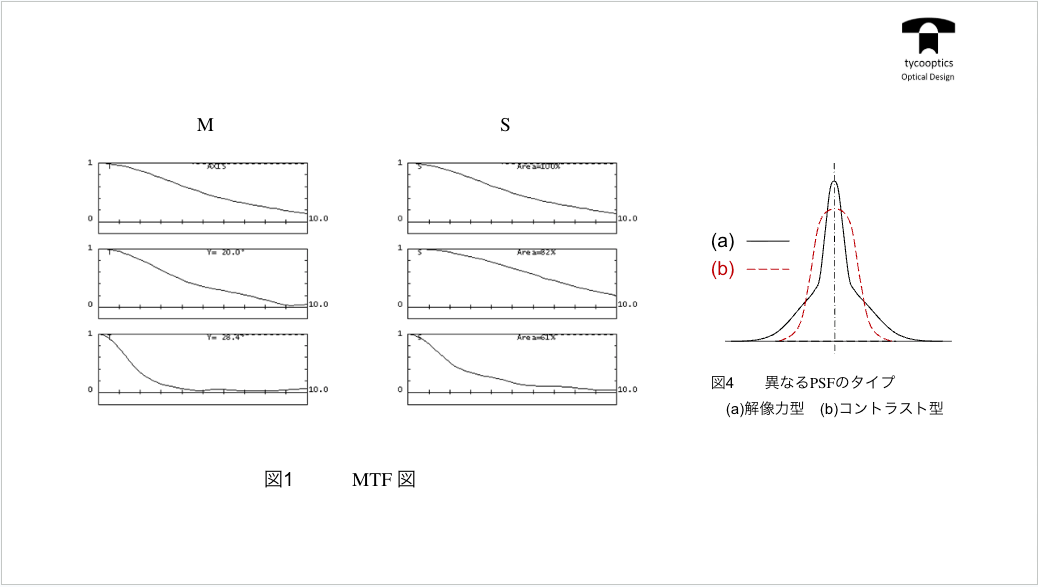
【球面収差図】
球面収差図っていうのをお話させていただきたいなと思います。ドイツと日本ですごく主に重宝がられてる図なんですけども、もちろんドイツでできたものだからかなとは思いますけども、この図で特許なんか見ると必ず大体このグラフが出てると言っていいと思います。
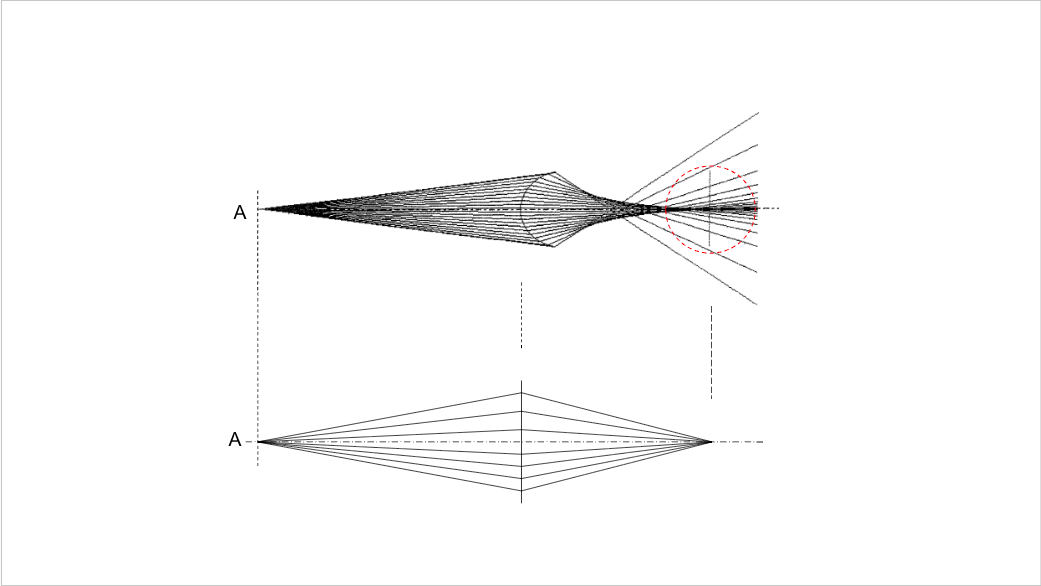
【球面収差図とそれに対応する点像の広がり】
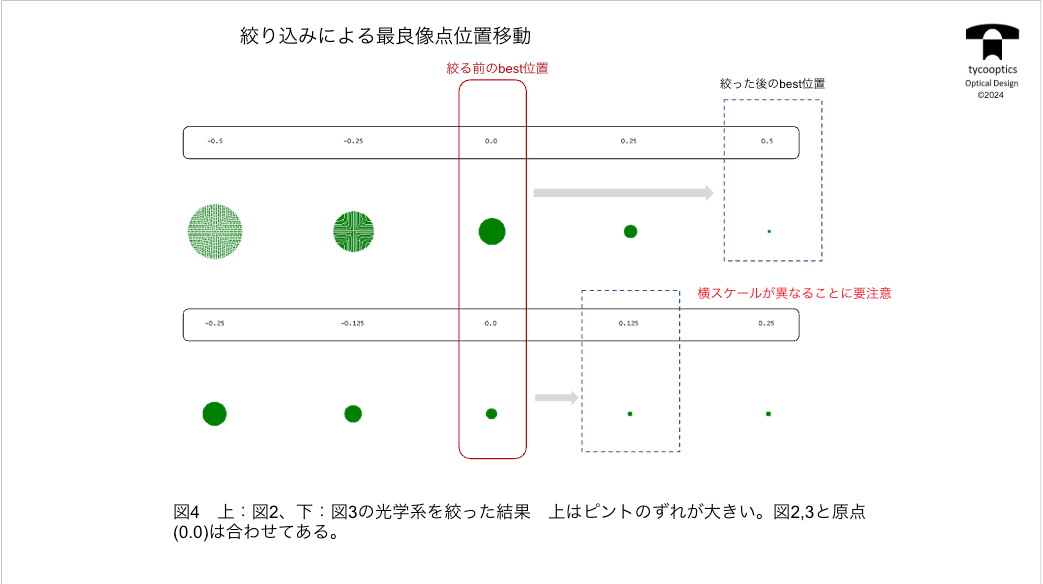
これ球面周波数なんですけども、設計者の技術によって、これをいろんなタイプに変えて、用途によって変えていくということになりますんで、今回もこういう球面収差で補正すると、フィルムの位置をどうどこに置くかによって点がどう映るかっていうシミュレーションが面白いんで見ていただきたいと思います。
【球面収差とコマ収差】
いよいよ軸外の話をいたしましょう。球面収差というのは、光軸上に物体がある場合の光の集束の具合を表してるもので、光軸上にあって物点が無限円にあれば、こういう光軸に平行な光線が同属光線として入ってくることになります。
【軸外の結像について】
ちょっと3次元的になってくるんで、軸上だとレンズが回転対称であれば収差も当然回転対象になるということになりますが、軸外結合については対称性がなくなっちゃうということですね。
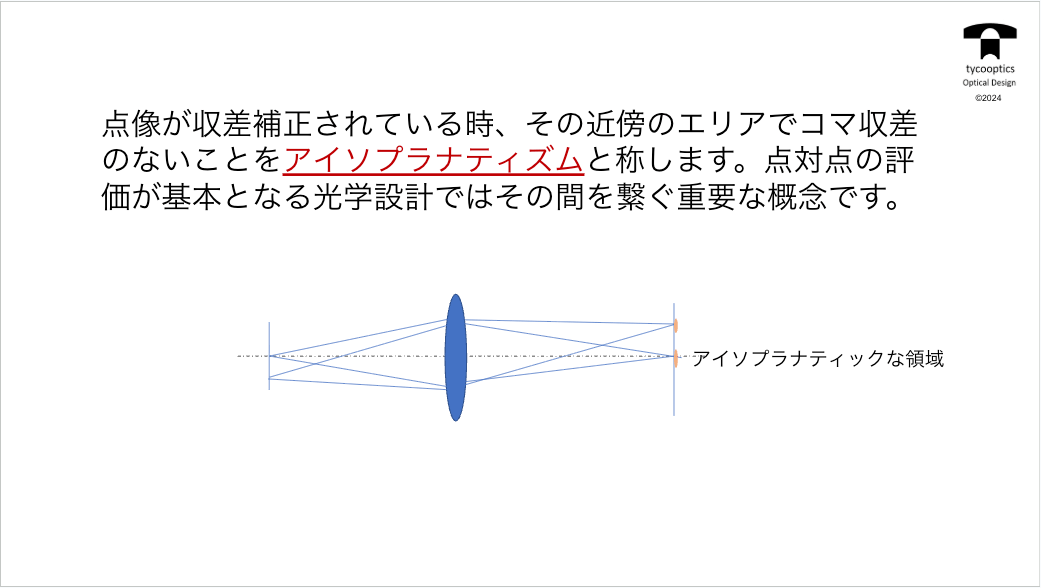
【アイソプラナティズムな領域】
この制限条件と覚えておいていただきたいんですけども、実はこれ、意識して設計している人はもうあまりいません。このアイソプラナティズムな領域っていうのは、コンピューターの最適化、自動設計ってものによって、自動的にある程度の範囲に保たれるように設計されています。
【ガウスの近軸理論以前の結像式】
ガウスの建築理論って19世紀になってからですけど、これ以前18世紀か、1700年代にもうレンズメーカーの式で使ってたんじゃないかと僕は推測してます。
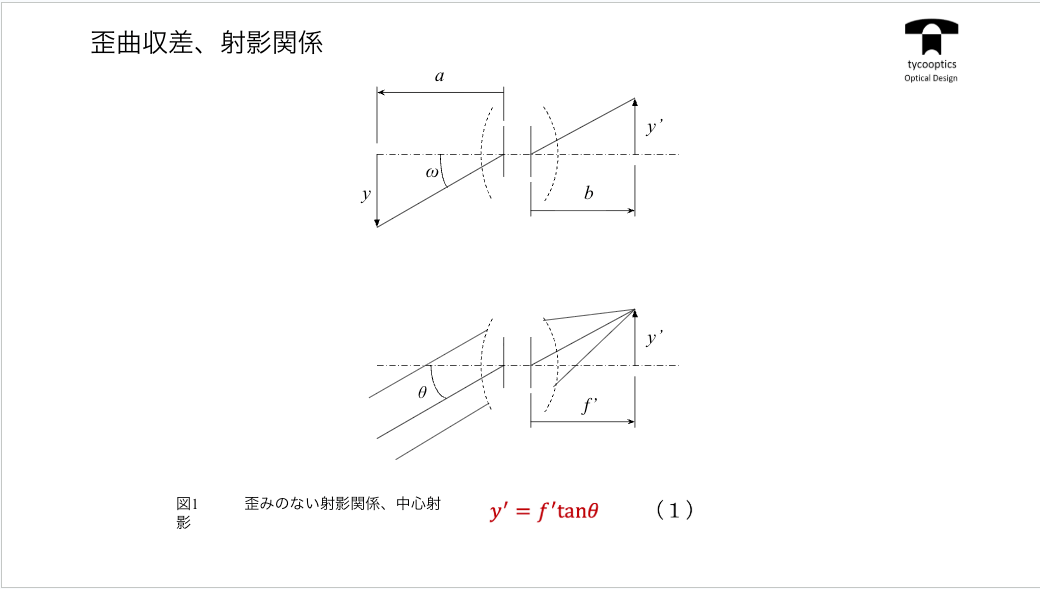
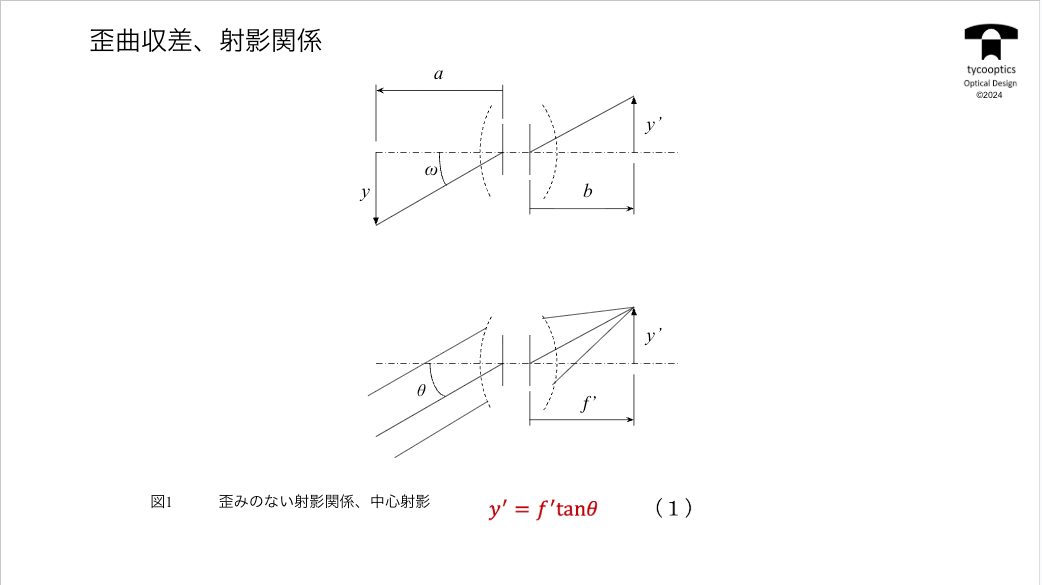
【歪曲収差と射影関係】
今まで球面収差、コマ収差、視点収差増減、湾曲とやってまいりました。最後に歪曲収差と射影関係についてお話していきます。
【質疑応答】
Q: 収差ついて、ソフトで設計をされる場合に 1番重要とすべきものや順番はありますか。
収差の表現の仕方:レンズの性質を知る上で重要な種々の図の読みとり方
【はじめに】
本日は収差の表現の仕方、レンズの性質を知る上で重要な種々の図の読み取り方ということについてやらせていただきます。
【光学設計の歴史と発展】
光学設計の歴史と発展の年表に照らし合わせて話しますと、今回は理論によって設計した時の収差の表示の仕方です。どこがっていうのはなかなか難しいんですけど、色消しレンズの理論というのはかなりこういう収差にとっても関係してきます。ここら辺の収差を良くするための理論が影響してきています。
【PCによる光学設計プログラムの機能変遷】
光学設計の歴史っていうのはPC、あるいは汎用コンピューターでもいいんですけど、1960年以降は光学設計プログラムの機能がどう変わっていったかということにかなり影響を大きく受けています。こういうものが大事となります。
【光学系(レンズ)設計開発に必要な能力分野】
前回レンズ設計の仕事で、収差をなくすことを申し上げました。レンズの収差をなくすことにかなりの時間を費やすのは確かですが、実際どうやるのか、そこの技術はどういう風に捉えたらいいですかという質問がありました。
結局は最適化で良くするという話をこれからしていきます。
【球面収差の説明】
前回と重複するのですが、球面収差というのが収差でありました。この1点から出た光が交わらないということ、これが一番基本的な収差です。
【スポットダイアグラム】
スポットダイヤグラムの説明です。
【ガラス産業の重要性】
球面収差の取り方もちょっとオーバーラップしてしまうのですが、これも前回やっています。クラウンフリントガラスによる色消しレンズの製作というのは1750年ぐらいにも制作されています。色消しレンズダブレットというのが作られ、C線とE線の色消しになってるものです。
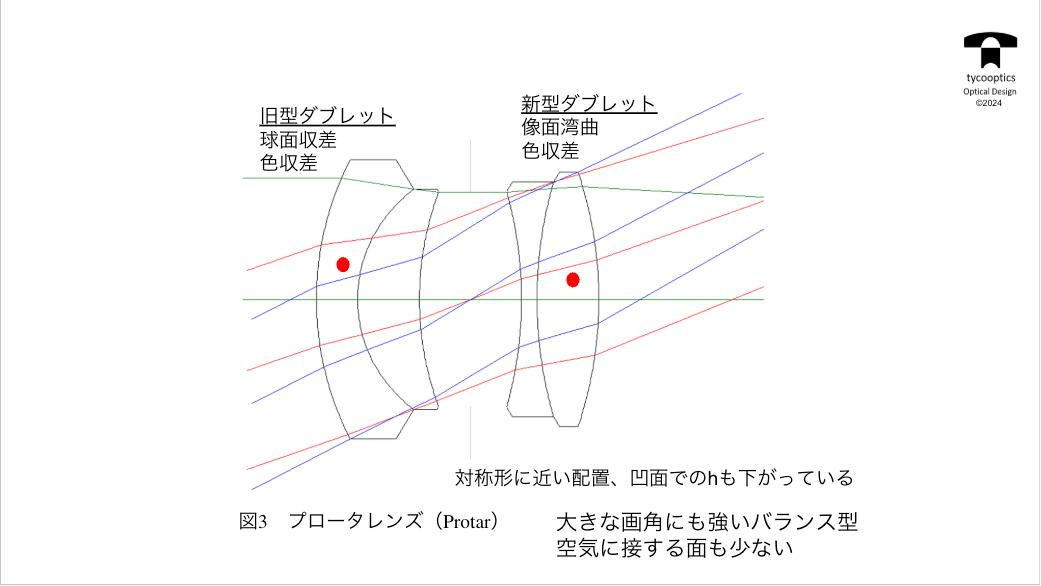
【旧型ダブレット】
旧型ダブレットの説明をします。
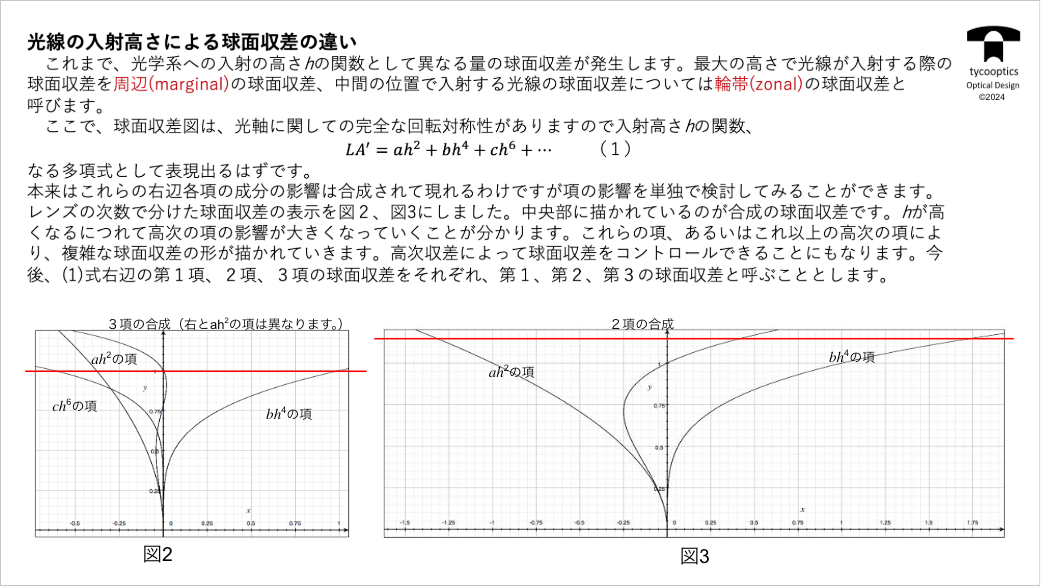
【球面の入射高さによる球面収差の違い】
球面収差が一番基本的な収差であるということはご紹介していますが、コマ収差も光源が軸上にあるのが球面収差です。しかし、それを軸外に持ってくると、同じ理屈によってコマ収差も発生しているということが説明できます。
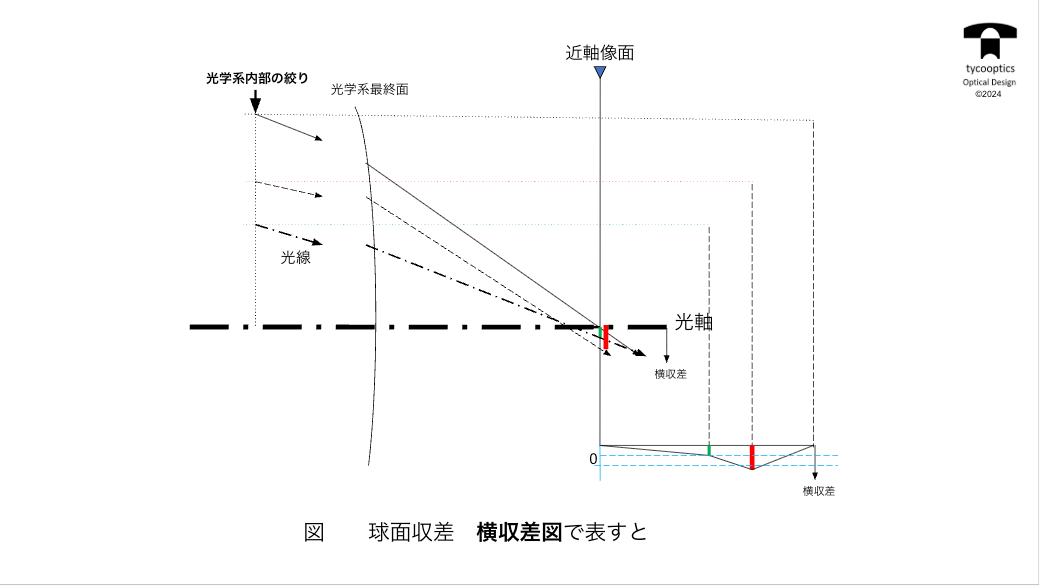
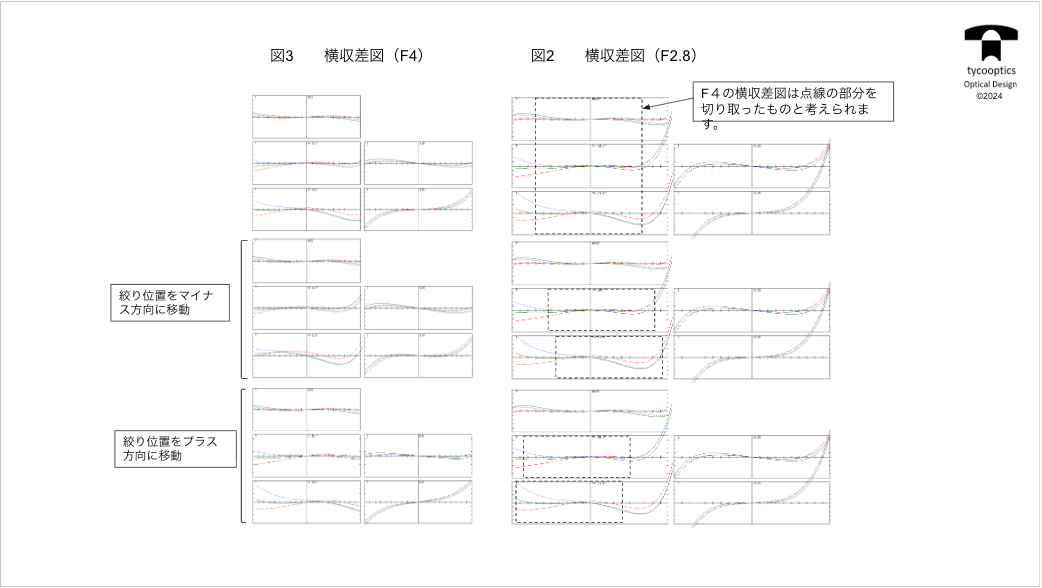
【横収差図】
特許やレンズの性能をよく見る時によく出てくるものが横収差図です。
これは絶対に読めた方がいいもので、設計しない人でもこれが読めるとレンズがどうなっているかということが分かりやすくなります。
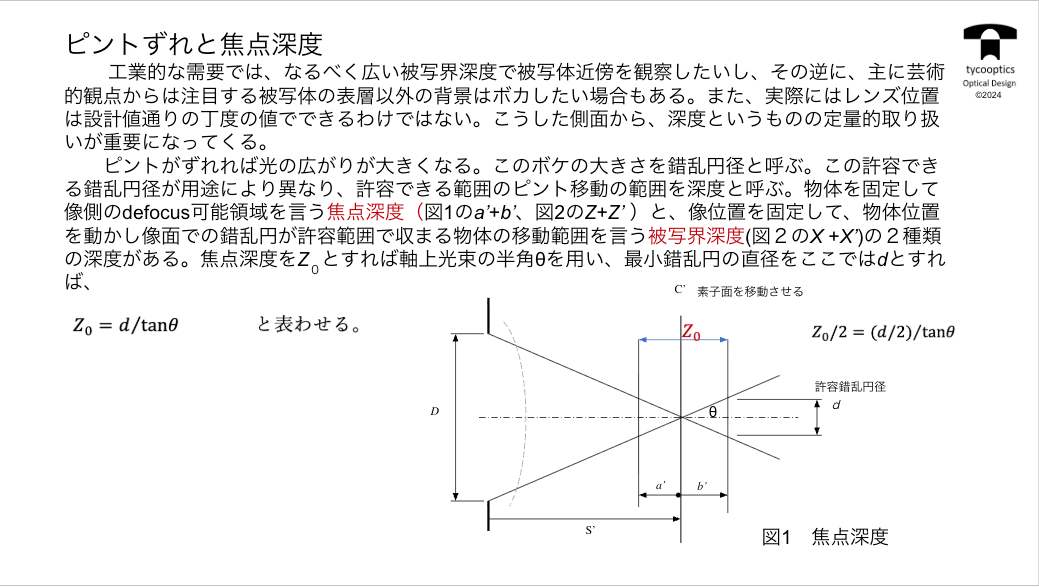
【ピントずれと焦点深度】
実際に皆さんがレンズを使う時、焦点深度は非常に重要になってきます。
例えば、上面がずれる、あるいは物体がずれた時に、どのくらいずれたものまでちゃんとした画像が得られるかということですね。
これは実際にレンズ系を使おうと思った場合には、結構重要な話になってきます。
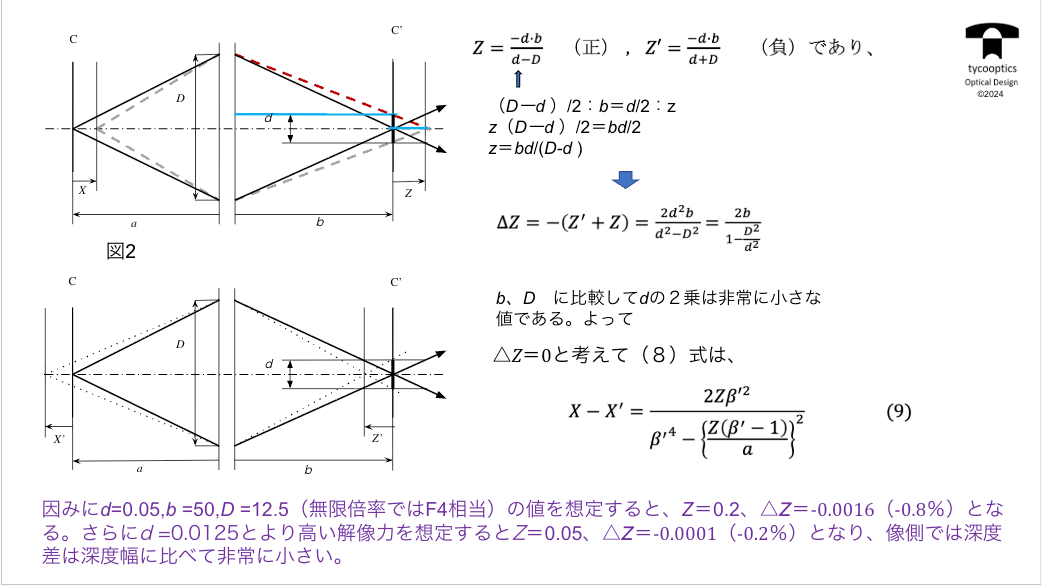
【被写界深度】
被写界深度についての説明です。
フィルムを固定した場合に、撮影しようとする物体がずれることがありますよね。
被写体のずれがどのくらいまで、ずれてもいいのかというのが被写界深度です。
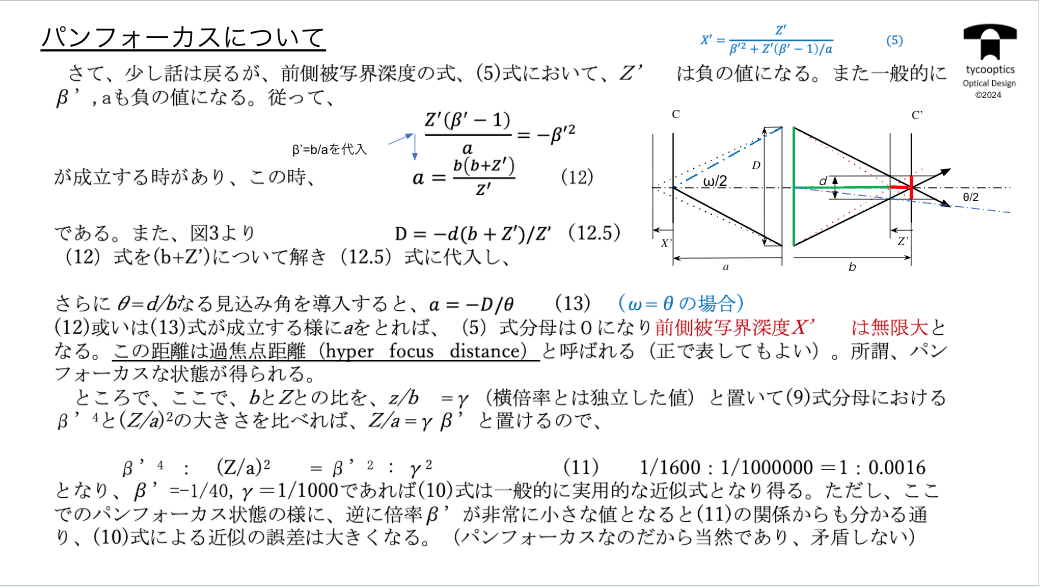
【パンフォーカスについて】
前トピックで出てきた式ですが、ある領域で被写界深度が無限大になる場合があります。
ある状態にしておけばそこから先は全てピントが合ってしまうという、これがいわゆるパンフォーカスな状態です。
【素子サイズと被写界深度】
このトピックスで一番申し上げたかったことについて話します。
デジタルカメラなんかで、撮像素子の大きさが撮影に与える影響というのは、カメラを使われる方は実感されてるかなと思います。
結局撮像素子が小さくなると被写界深度が深くなるといわれてます。
収差・性能を良くするための幾つかの理論、戦略、定番のレンズタイプ
【はじめに】
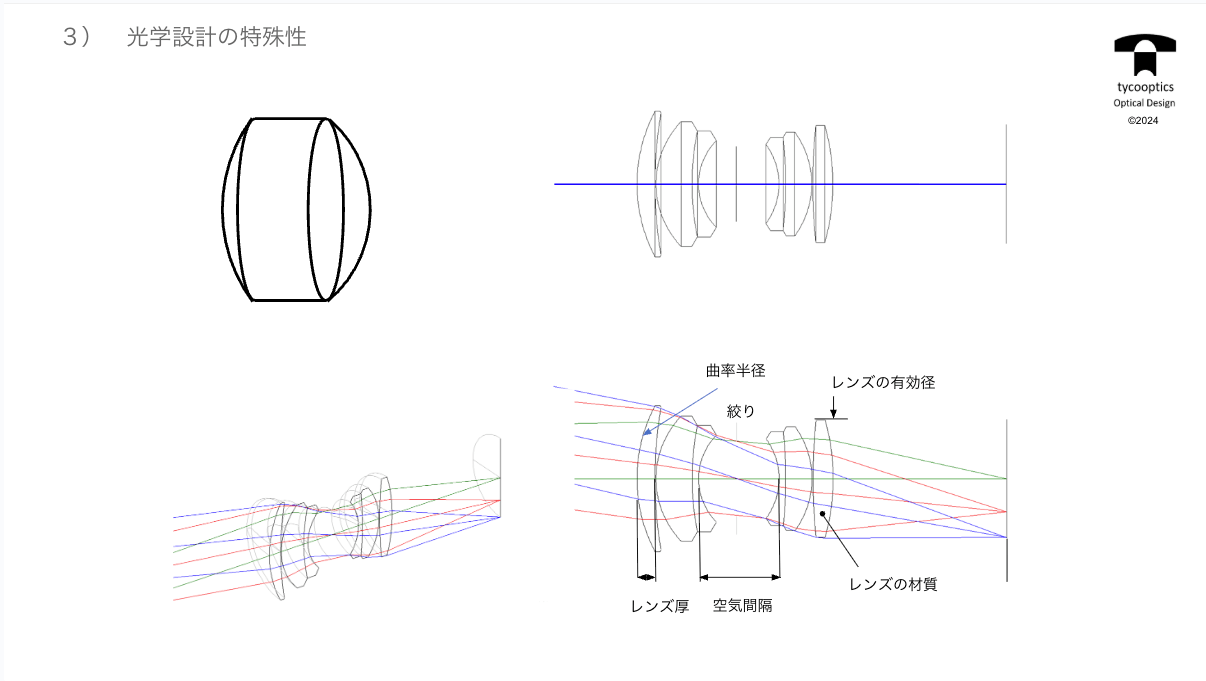
今回は収差・性能をよくするためのいくつかの理論と戦略、そして定番のレンズタイプについて説明します。ここまで基礎理論的なことをずっとやってきましたが、では具体的なレンズとしてはどういう形になるのか、あるいは今まで使ってきた理論をどう役立てるか、レンズというものをどう考えればいいのかということをお話ししたいと思います。
【光学設計の歴史と発展】
光学設計の歴史と発展に沿って、これまで話した色消しレンズについてはもちろん、新種ガラスやザイデルの3次収差論などについてもお話ししていきます。
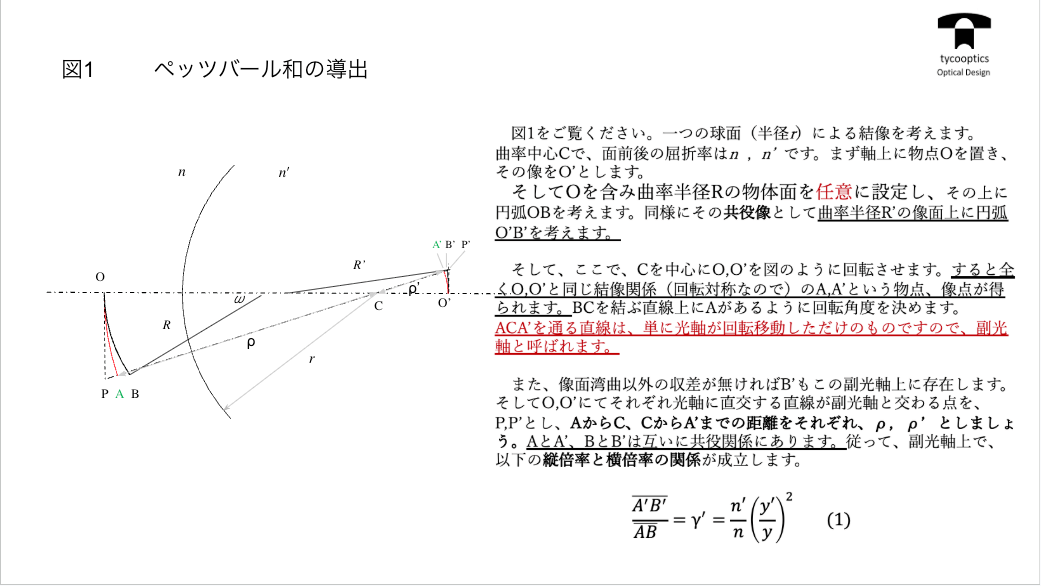
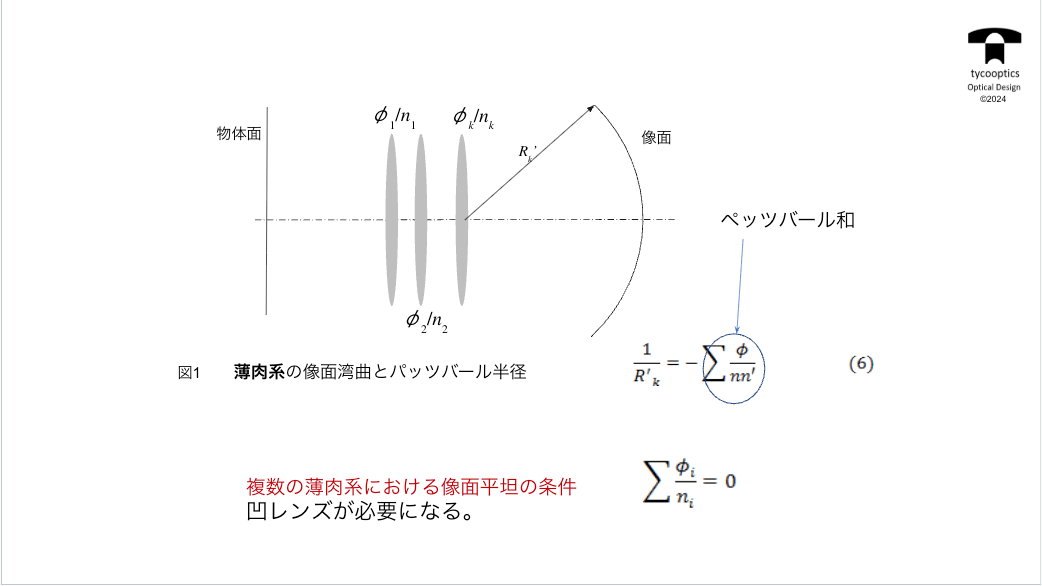
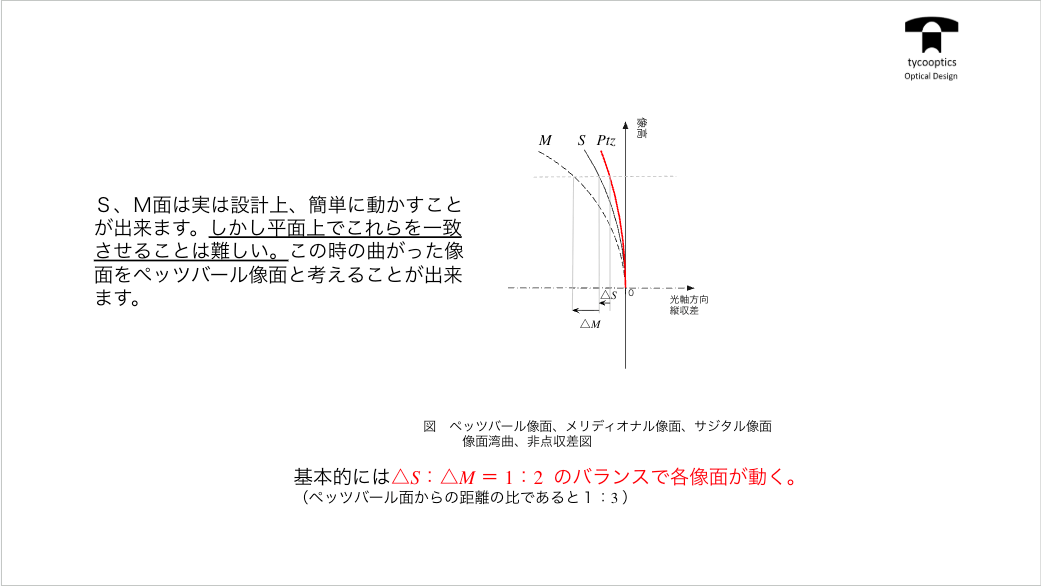
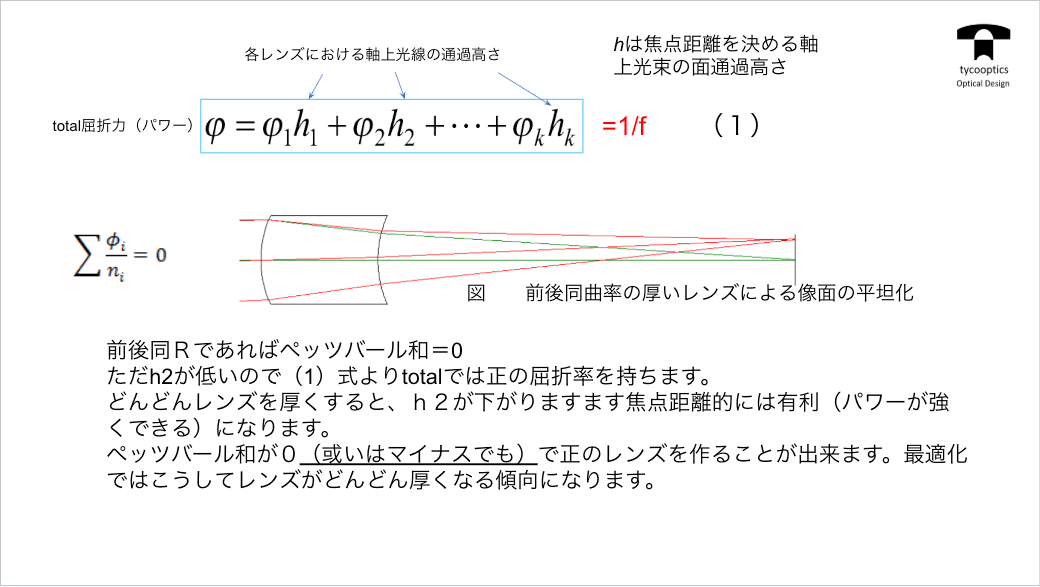
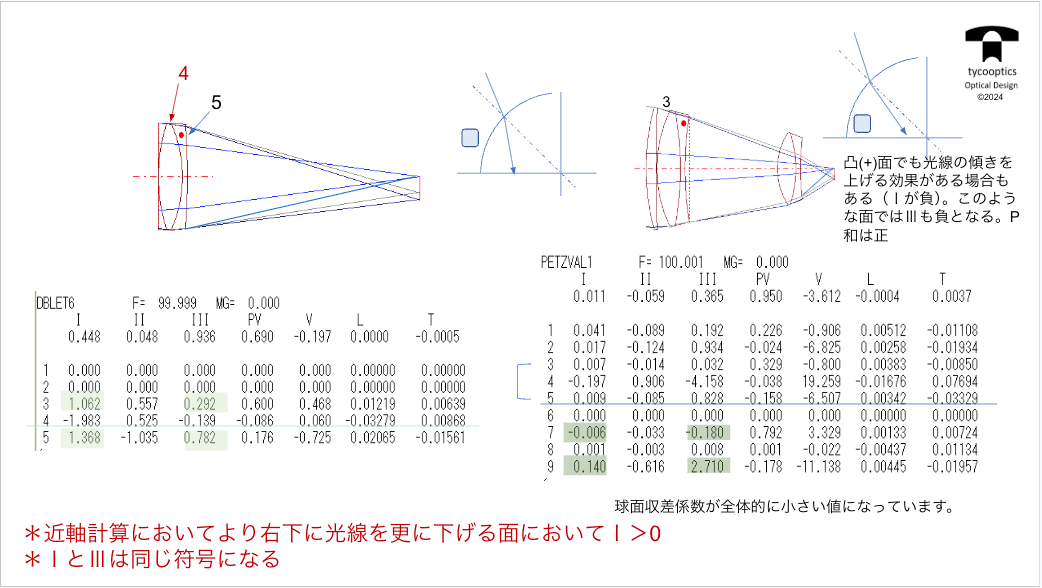
【ペッツバール像面】
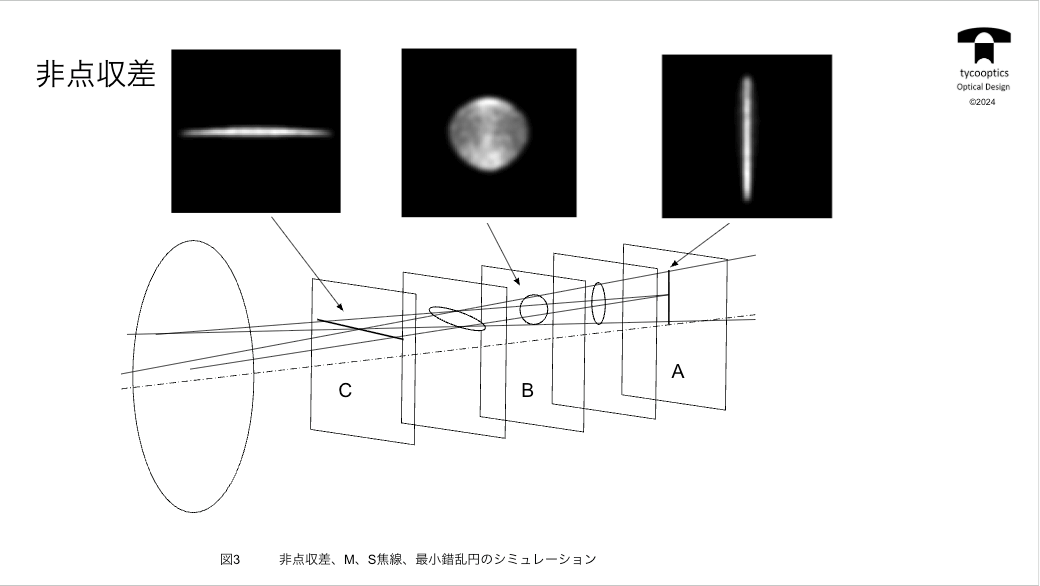
これまでもレンズというのは像面湾曲が起きるというお話をしました。どういうことかというとフィルムとか撮像素子は真っ平らな面でなってる場合が多いです。その場合、レンズによる結像が同じく真っ平らな目に映るのがいいんですけども、どうしても手前に曲がってきてしまう、または奥に曲がって反ってしまうってこともあるんですが、平らにならない。その時、「ペッツバール像面」というものを考えます。
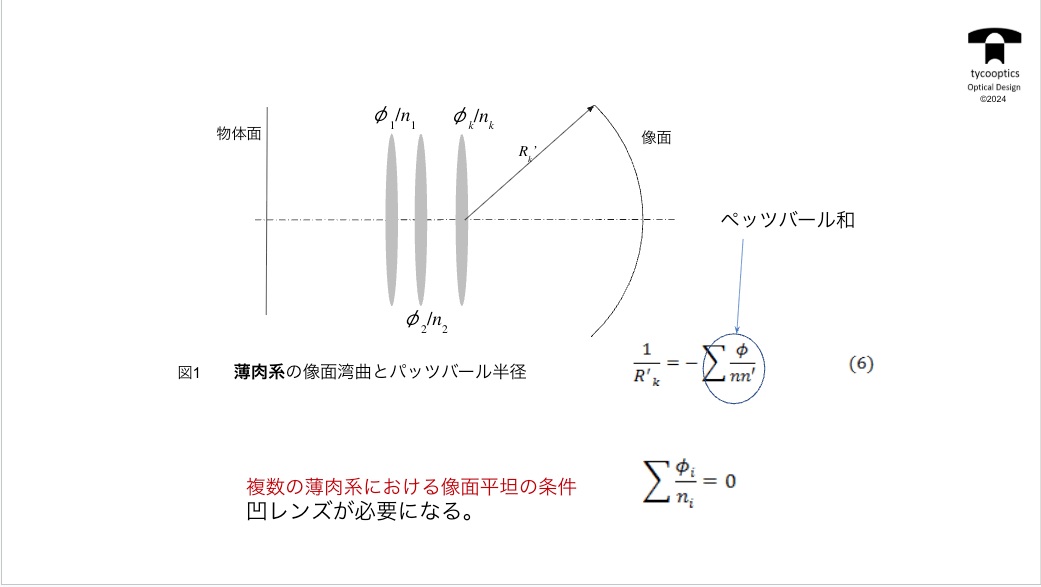
【薄肉系の像面湾曲とペッツバール和】
ピッツバーグ像面の曲率とはそれぞれの面のパワーで光を曲げる力ですね。各面の光を曲げる力。これこれをその面の前後の媒質の屈折率で割ったものです。曲率なんで0になる方がいいです。半径でいうと無限ということになりますから、そうしますとペッツバール和をなるべく0に近づけたいということになります。
【レンズの焦点距離とパワー(total屈折力)】
レンズというのは大体、収束系が多いです。結合させるっていうことは、つまり屈折力もプラス、光を集める力がないと結像できないのです。凹レンズだと光が発散しちゃいますので、もちろんそれはそれで役割は果たせるのですが、1つの完成品としてレンズを考えた場合には圧倒的に結合するものが多いわけです。
【3つのレンズ】
レンズ設計をやられている方はおわかりになると思うんですけど、機械任せで最適化をすると、どんどん厚いレンズを作ってくる設計になってきます。そうしますと、これは一つの収差論の応用というか、論理的な設計の一つなんですよね。これをこのトピックでは、普通の組み合わせレンズについて考えてみようと思います。
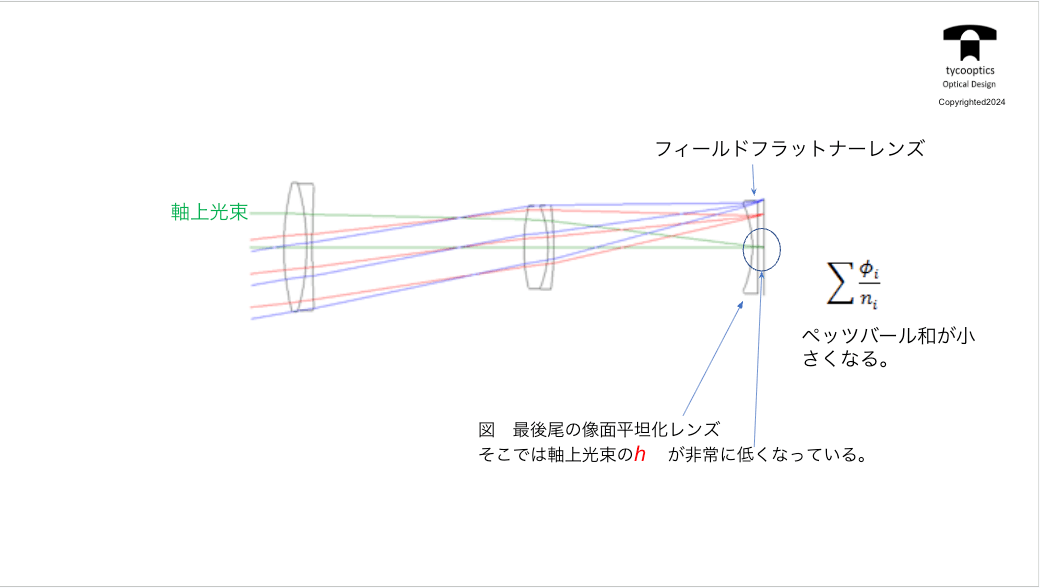
【フィールドフラットナーレンズ】
今のところ像面湾曲というのは光学設計にとっては非常に重要なところです。それはなぜかといいますと、顕微鏡なんかももちろん像面は光を観察する範囲は有効な範囲があるからです。特に写真レンズや、マシンビジョン、そういうものは広い範囲を観察しないといけないので、像面湾曲を撮るということは非常に重要になっています。
【フィールドレンズ】
フィールドレンズについての説明です。
【ペッツバール和の重要性】
ペッツバール和の式は単純故に重要な性質をもっています。ここで、一つお話ししておかなければいけないことが、ペッツバール和も近似の結果であるものだということです。
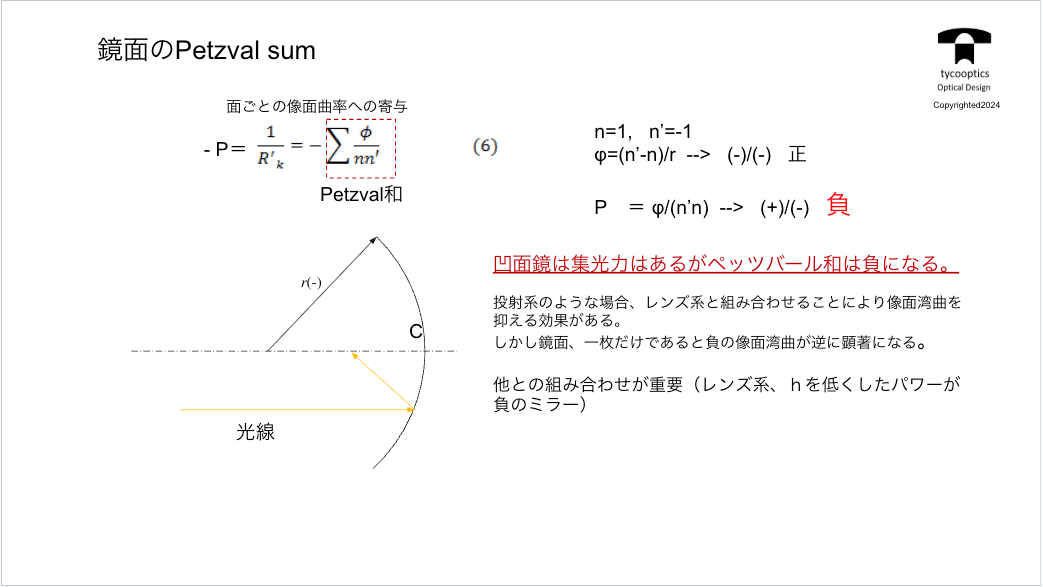
【鏡面のペッツバール和】
プロジェクターや望遠鏡、色んなもので鏡を使います。今までレンズの話をしてきましたが、鏡面のペッツバール和はどうなるのかということについてお話します。
【球面収差を除去する方法】
球面収差をどうやって除去するかという方法についてです。これはもう既にお話ししているのですが、今一度整理してみました。これをどのようにして実際の光学系に使っているのかというお話をしていきます。
【具体的なレンズ構成の基本構造】
球面収差を除去するために、具体的にどのようなレンズが必要かということについて話していきます。
【3つ目の除去方法:負のパワーを用いる】
球面収差を除去する方法の3つ目「負のパワーを用いる」という方法について説明します。
【旧型ダブレット】
前回接合面で負のパワーを持っているとコントロールしやすいかということについて少しお話ししました。もう一度言わせていただくと、このダブレットの色消し条件というのは今日のお話とは全く別で、ダブレットで焦点距離の色を取るためにはある条件を満たさなきゃいけないのです。
【プロータレンズ】
2つのレンズをくっつけた新型ダブレットができてきて、最初に実用化された画期的なレンズというのが、このプロータレンズです。
【さまざまなレンズの例】
どのようなダブレットとして使われているのかということに関して、いろいろな例を挙げていきます。
【収差補正のための基本事項】
ここまでお話した収差補正のための基本事項について整理します。
【光学設計の流れ】
この流れ図は前にもお出ししましたが、結局は光学設計はこういうサイクルになっています。仕様が決定され、基本配置を考え、収差補正を行ない、評価を行い出図という流れなのですが、これはいっているほどうまくいかないです。
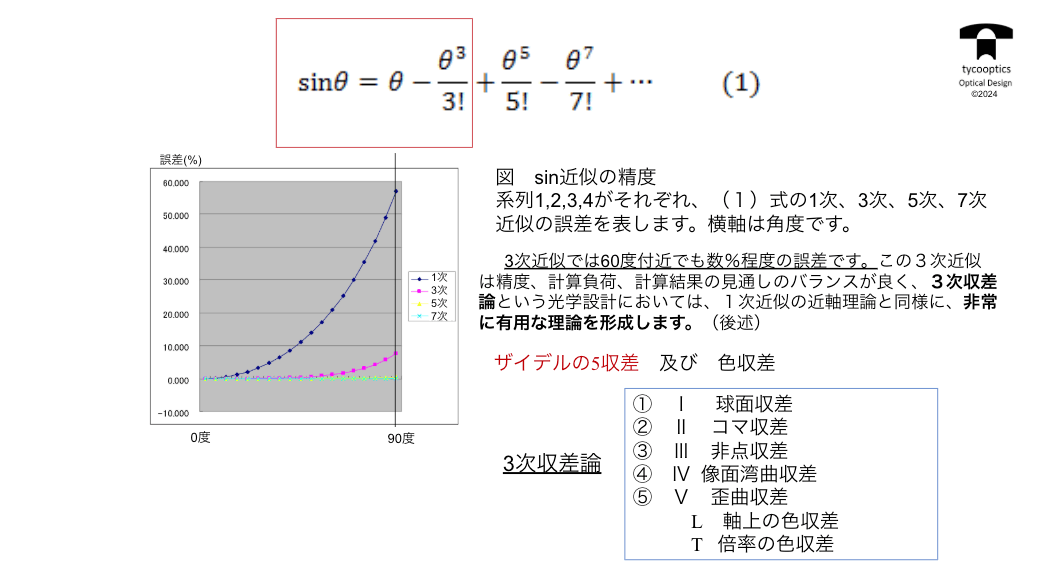
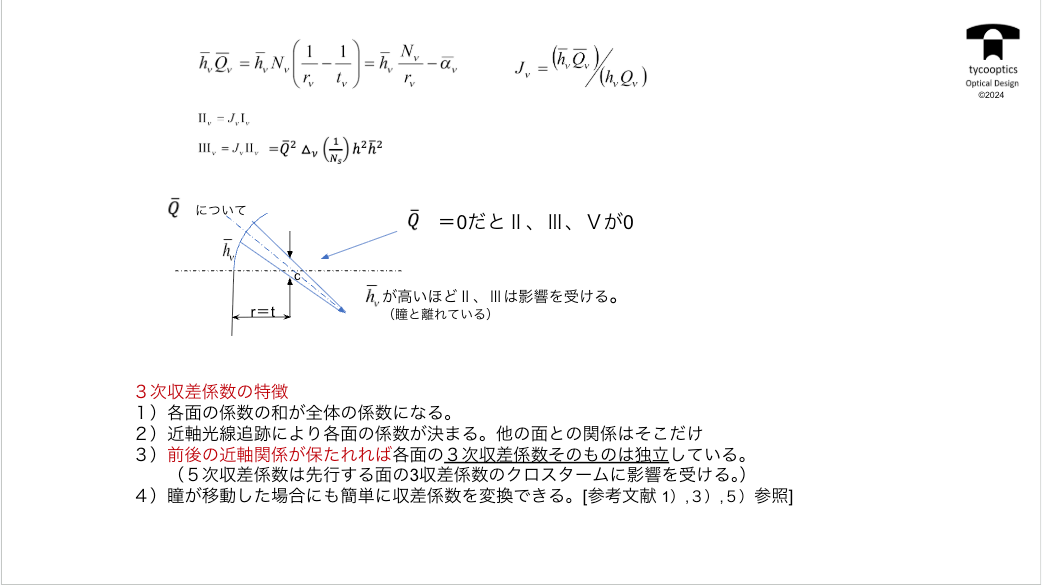
【ザイデルの5収差および色収差】
3次収差論とは結局何かいうと、機械工学の話なので所詮sinθをどう計算するのかということに話はつきます。
【3次収差による横収差表現】
3次収差による横収差表現の解説です。
【3次収差係数(球面)】
3次収差係数(球面)についての説明です。
【質疑応答】
Q.1 瞳収差のことで、レーザーのビーム系にもよりますが、どこに入射するかによって変化するということでしょうか?
波動光学的結像理論:レーザー光学系の設計について
【今回の講義内容】
今回で収差・補正をどうやってやるのかということや、収差とはどういうものかという、レンズ設計で一番時間がかかってしまうところは一応この回で終わりにしたいと思います。
今回の付録は、最後にレンズを全く0から作るときに、今までレンズというもののがどうやって発展してきたかということを、今までのお話も参考に思い出していただきながらその進化の過程を説明していきたいと思います。
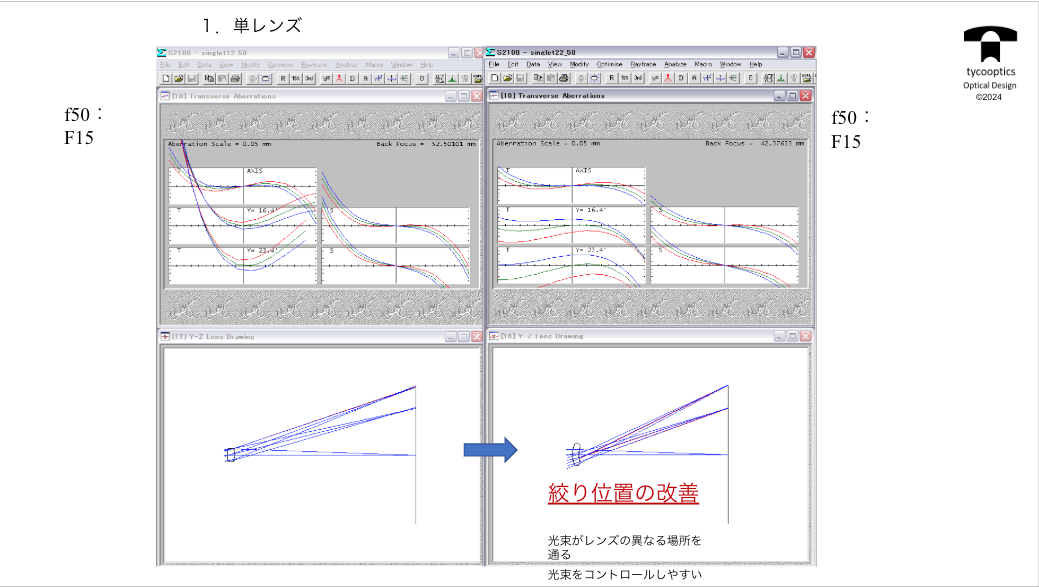
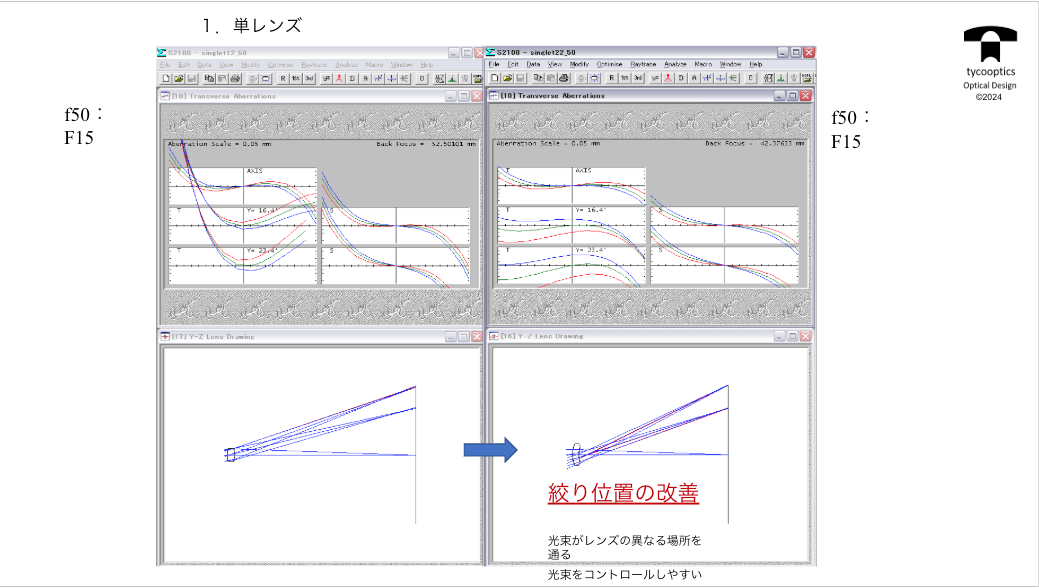
【付録:単レンズ】
全く0から出発しても面白みのある「どうやってレンズって何枚も増えてきたんだろう」というところにスポットを当ててお話しさせていただきたいと思います。
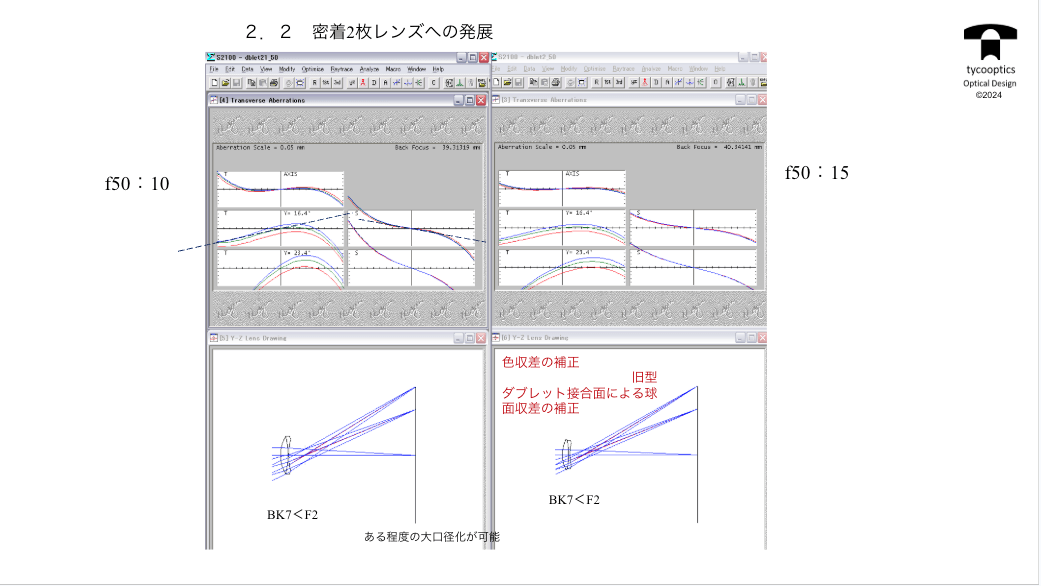
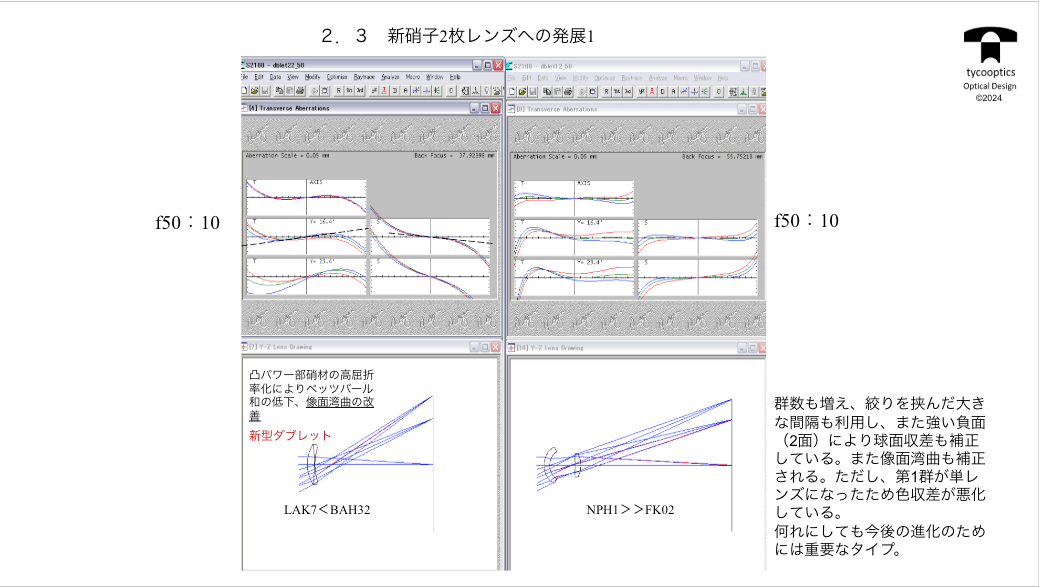
【新硝子2枚レンズへの発展】
話は時代的にはちょっと飛んでしまうのですが、ショットからですね、凸レンズで非常に高屈折率のガラスができたということで、旧型ダブレットでは凹レンズの方の屈折率を高くして、凹レンズの屈折率を低くするっていうのが旧型タブレットでした。
復習しますと、旧型ダブレットの特徴は接合面が多めになるので、球面収差が補正されるということになるわけです。
では新型ダブレットの特徴はどんなものになるのでしょうか?
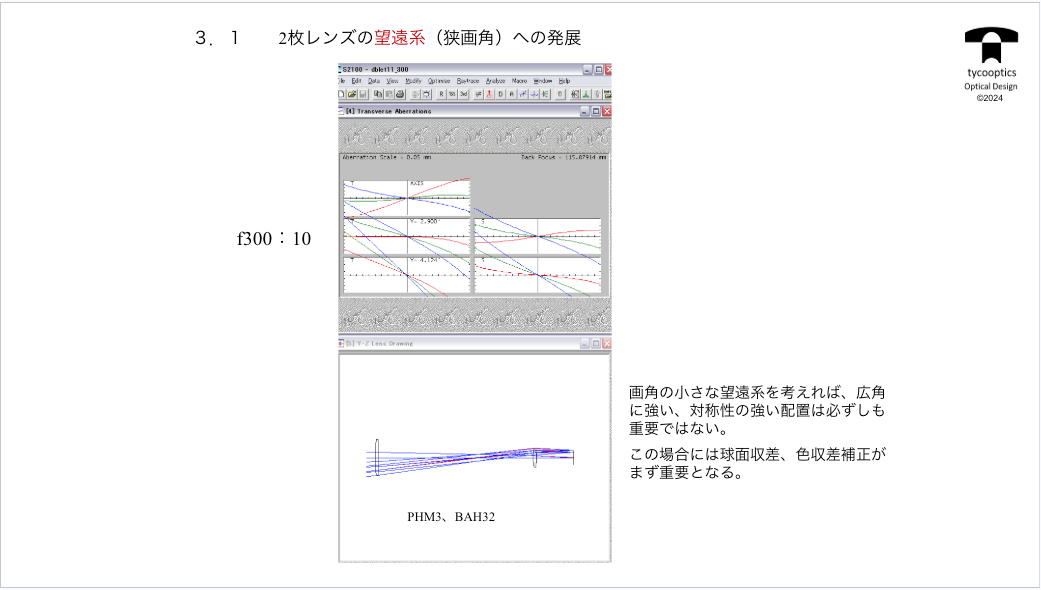
【2枚レンズの望遠系(狭画角)への発展】
望遠系とはどのようなものなのでしょうか?
大きく見るためのものですから、フィルムの中にあんまり多くの画角を取り込んでしまうと、情報量としては同じですから、画面中心付近の情報は薄くなってしまいます。
【2枚レンズの望遠系における3種類の分離】
1面ダブレットを1ブロック、1群だけで構成するとどうなるのでしょうか?
【2枚レンズ群の対象型配置、分離等の発展】
2枚レンズ群の対象型配置、分離等の発展についての説明です。
【2枚レンズ群の対象型配置、分離後の更なる発展】
2枚レンズ群の対象型配置、分離後の更なる発展についての説明です。
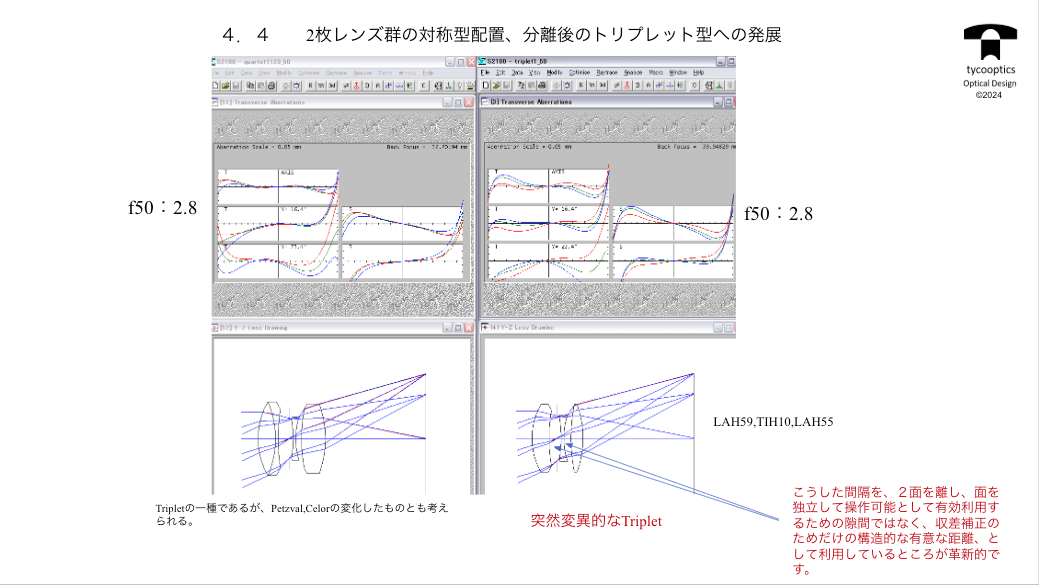
【2枚レンズ群の対象型配置、分離後のトリプレット型への発展】
いよいよトリプレットが登場してきます。トリプレットという名前にあるように3枚玉です。
もう一つトリプレットの1種、テッサー型のタイプがあります。
テッサーとは厳密にいうとダブレットが後ろ側に配置しています。
【2枚レンズ群の対象型配置、分離後(ガウス対物)の更なる発展】
2枚レンズ群の対象型配置、分離後(ガウス対物)の更なる発展についての説明です。
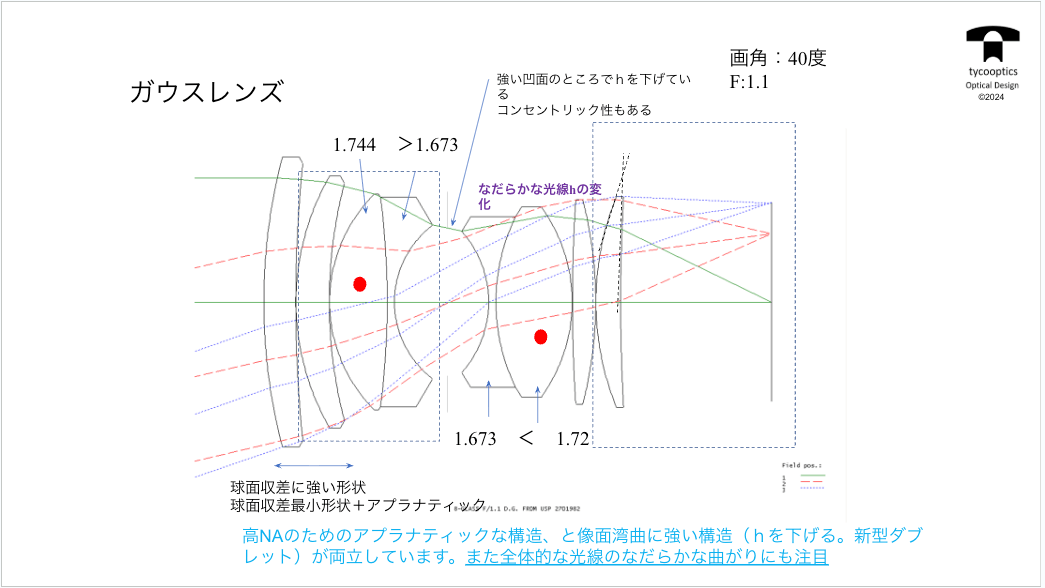
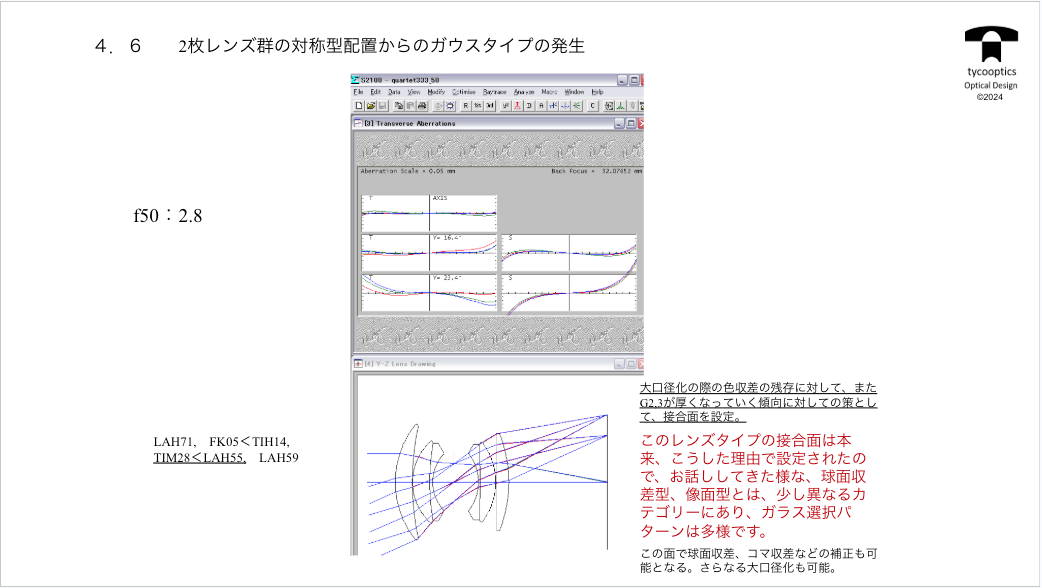
【2枚レンズ群の対象型配置からのガウスタイプの発生】
今の完成形のダブルガウスタイプについてです。いろんな特許を見ていただくと、これが本当にいろんなところに出ています。
接合面にして作りやすく、それからもちろん色収差も補正できますし、球面収差も補正できるということになります。
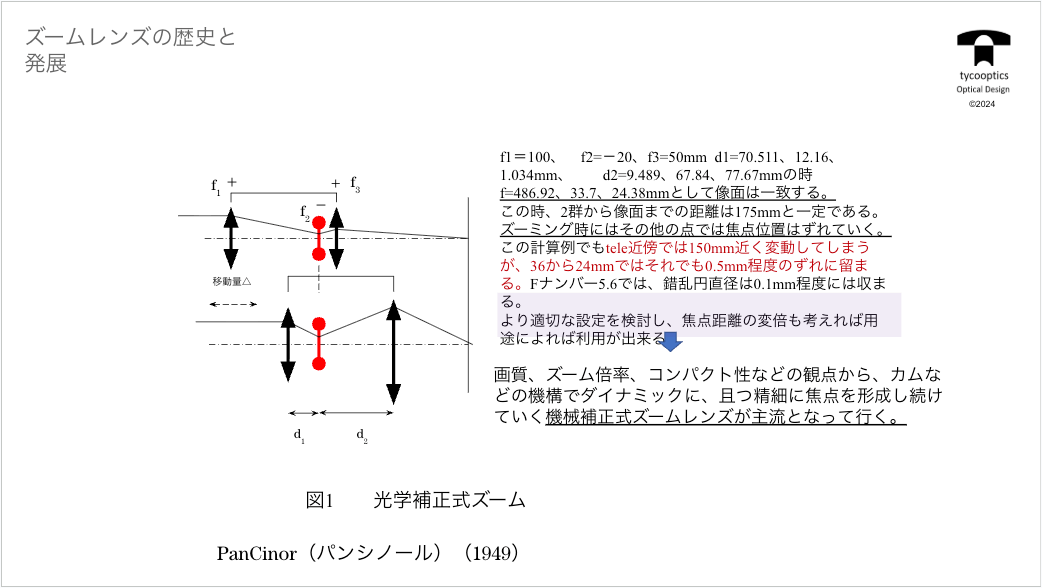
【ズームレンズの歴史と発展】
これからズームレンズについて、非常に簡単ではございますが、歴史・発展まで少し触れさせていただきます。
【2群ズーム】
原点に立ち戻ってみるとですね、一番簡単なズーム、何かっていうと2つのレンズがあります。
【2群ズームの例】
2群ズームの例を挙げていきます。
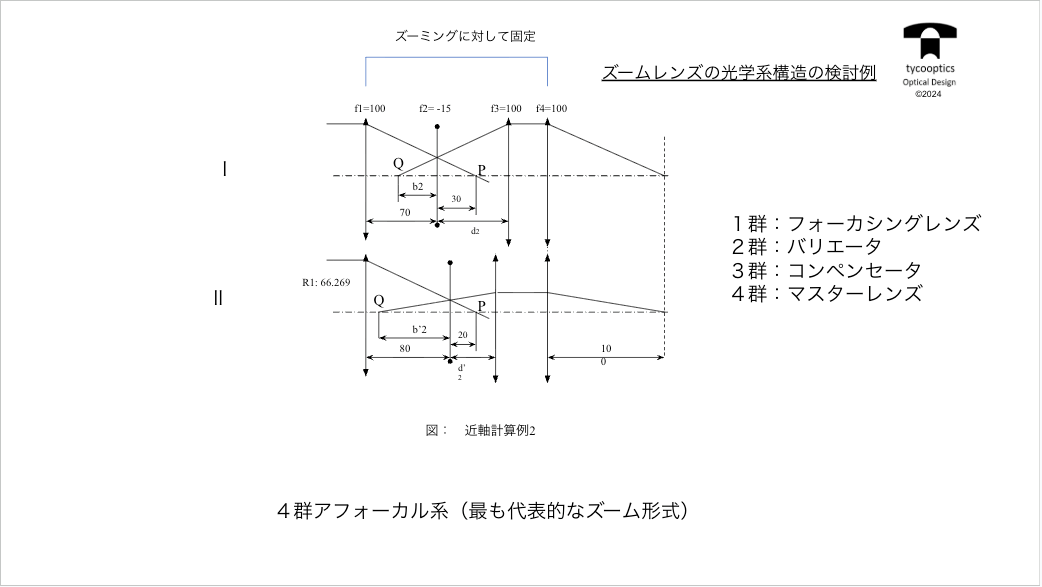
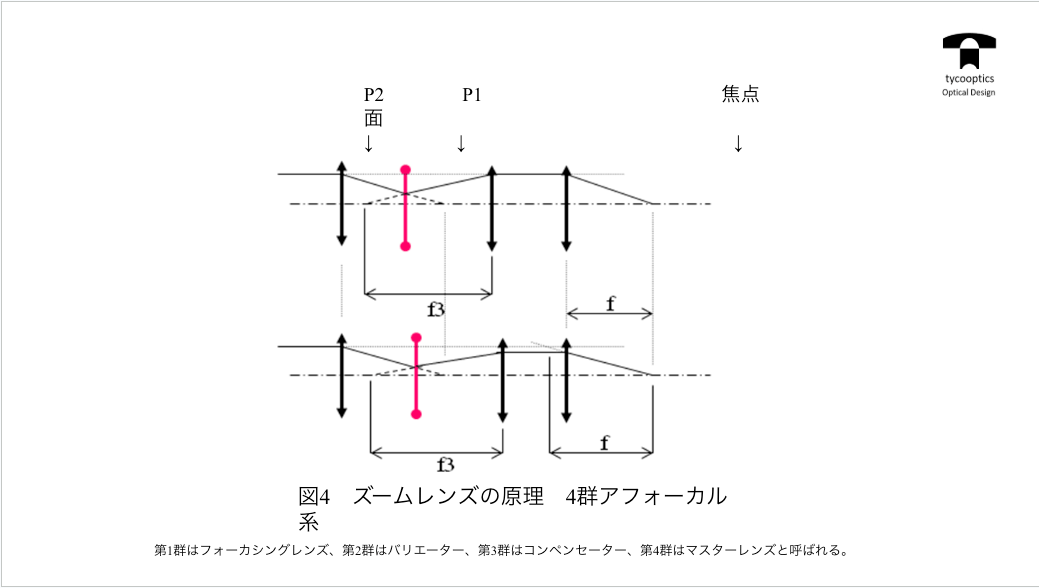
【ズームレンズの原理、4群アフォーカル系】
次の発想としましては、これは講義の本編でもお話ししてるんですけども。
いっとう最後の4群を一定の位置に置きます。像群と4群は常に固定です。
【4群アフォーカルズーム系】
4群アフォーカルズーム系についての説明です。
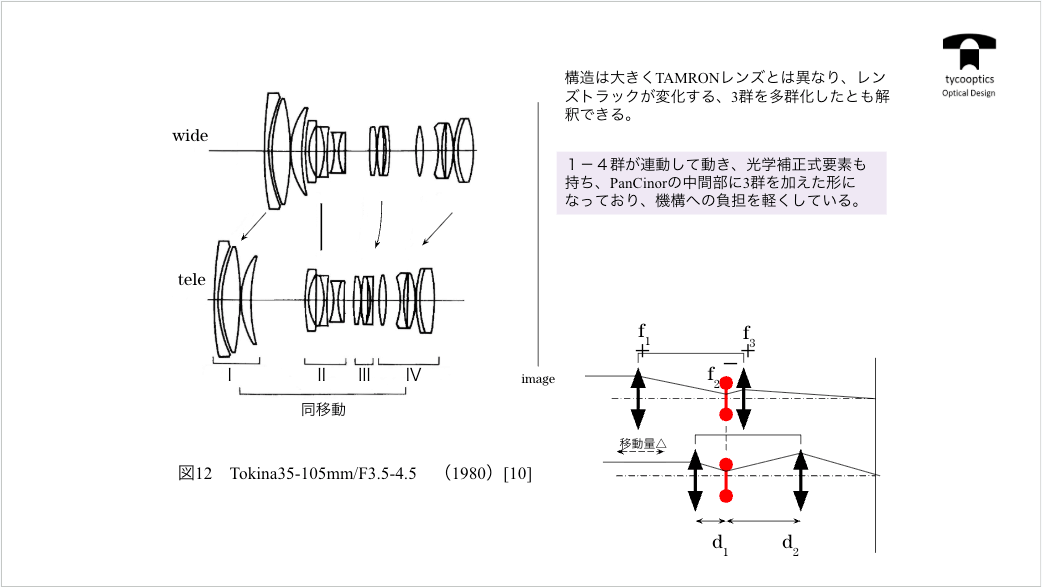
【Tokina35-105mm/F3.5-4.5】
高倍率を稼ぐためには、たとえば3倍なんていう高倍率を稼ぐためにはどうしたらいいのかということについてお話しします。
【ズームレンズにおける前玉繰り出しのメリット】
前玉繰り出しという一番玉だけ動かすということについてお話しします。
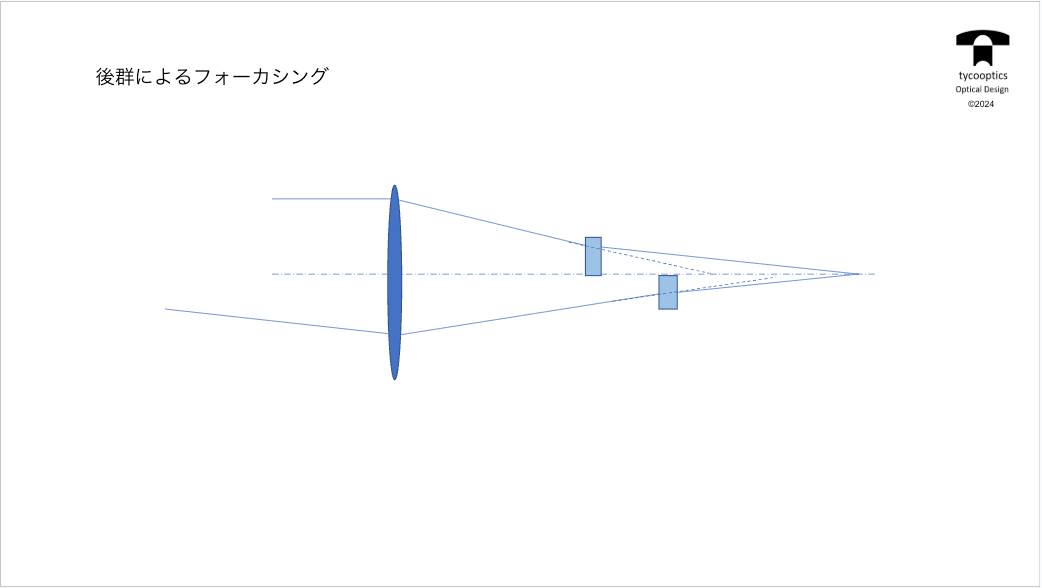
【後群によるフォーカシング】
前玉繰り出しの欠点といえば、1群が大きいことです。
場合によってはズーミングでも使いますし、前玉繰り出してフォーカシングにも使うわけですが、
少し大きいので、このためにリアフォーカシングということが考えられました。
【さらなる高倍率ズームへの発展】
TAMRONの中間フォーカスから始まり、
さらなる高倍率ズームへの発展についてお話ししていきます。
波動光学的結像理論:レーザー光学系の設計について
【本日の講義概要】
今回からは波動光学的な結像理論と光学設計というテーマでやらせていただきたいと思います。
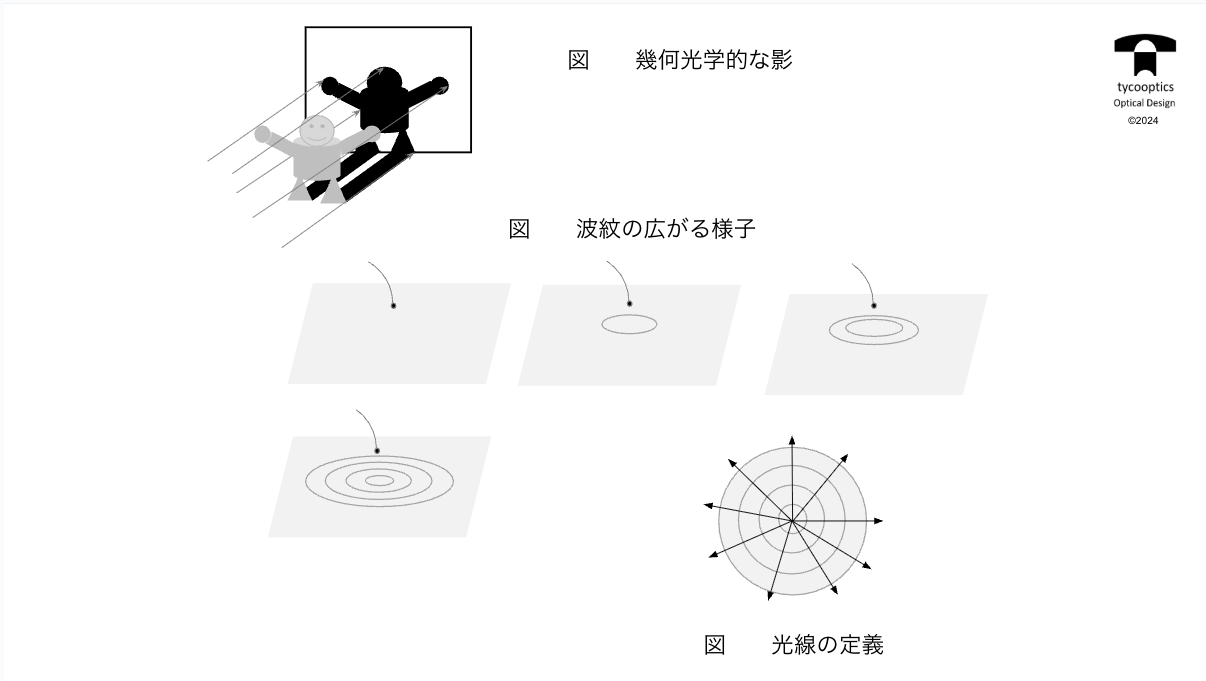
この講座の最初の頃に波動光学と幾何光学というお話をさせていただいたのですが、光学設計における幾何光学とは、光を1本の線の集まりみたいな形で光線の集合体として考えるというものです。
それともう一つ、波動光学として考えるというお話があって、だいたい光学設計の収差論的なところですとか、光学系の配置なんていうのを考えるときには、幾何光学で話をするということで、本講義第2回から第7回ぐらいまでは幾何光学の話でした。しかし波動光学的な性質でどうかということは、概念的だけではなくて、少し細かくお話しする必要があるかなと思います。
本講義の受講者の多くはレーザー系とかレーザー機器なんかを扱われている方というお話を伺ってます。
レーザービームとかを扱う場合には、どうしても波動工学的な知識がある程度必要になるということで、非常に本講座では重要なポイントとなってくると思います。
【光学設計の歴史と発展】
今回はフェルマーの原理、ホイヘンスの原理から電磁波電磁方程式を基礎としたところ、またフレネルキルヒホッフ回折積分という、大きな出来事についてお話ししていきます。
【参考文献について】
谷田貝豊彦(2024)『Pythonで学ぶ光学の基礎』朝倉書店
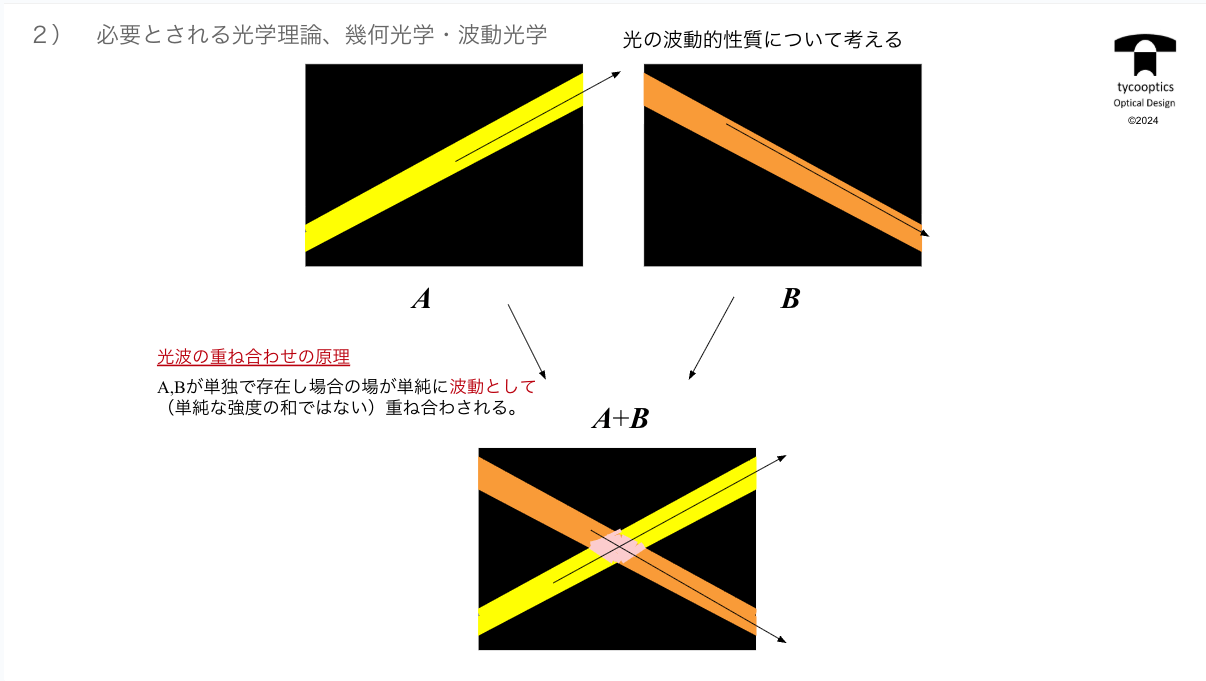
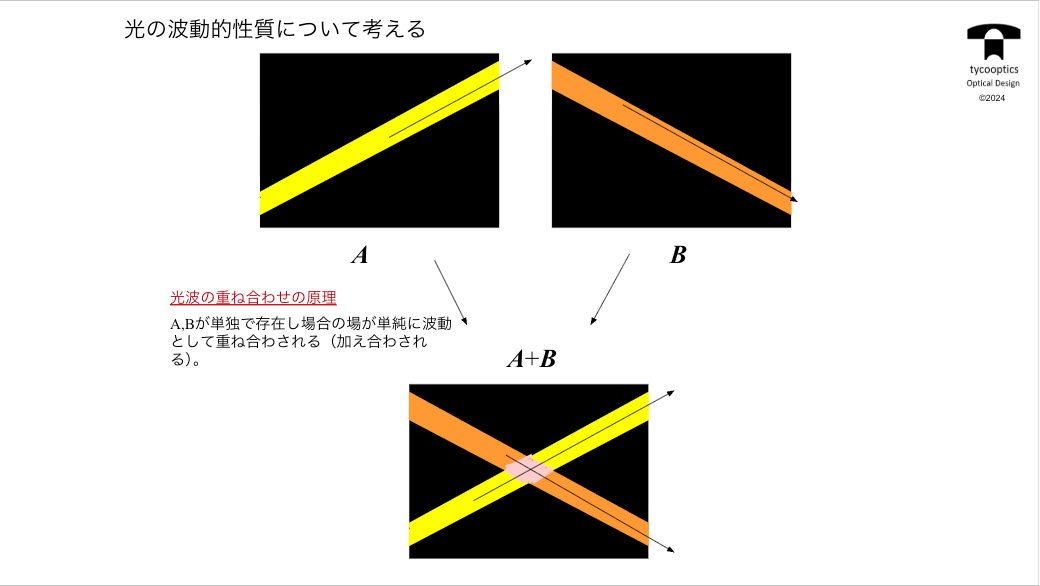
【光の波動的性質について考える】
波動光学は波。光が進むのを波が進むと考える。特徴は光波の重ね合わせの原理が成立すること。
【Youngの干渉実験】
有名な干渉実験ですよね。光学の本見れば真っ先にでておりますし、谷田貝先生も詳しく解説されてらっしゃると思いますし、あんまり細かく言う意味はないんですけど。
【円形開口の回折像振幅分布】
Youngの干渉実験とかなり似ているのですが、いろんな方向に光が散るっていうお話にいたしまして、これ簡単に言ってしまえば、ここの穴が小さければちっちゃいほど、いろんな方向に切る角度は大きくなります。
【これまでのまとめ】
波動光学的解析が必要な場合についてまとめました。
【1mm四方の結像のシミュレーション】
波動光学的評価と幾何光学的評価の違いについてです。大体1ミリ程度に光が広がった場合のシミュレーションを行ってます。光学設計において写真レンズって大体1点から出た光が30ミクロンぐらいの幅に納める必要があります。
1ミリですから、1点から出た光がこのくらい広がっちゃってる状態なので、かなり良好な結像状態とは言いにくい状態になってるわけです。
これをちゃんとどういう像になってるかって評価しようとすると、以上の違いが出てくるということです。
【波動の表現】
今一歩進んで「波」のお話はしておかなければいけないのですが、これはもう谷田貝先生(他セミナー講師)が十分されていると思うので、設計のための理論として必要な最低限のところのお話をしたいと思います。
【偏光】
もう一つ重要なのが偏光という概念です。正弦波、マックススウェルの方程式は、どこかの中の平面にですね、立体的な深度でもいいので、それを射影したときに正弦波に解がなっていればいいので、螺旋階段状に振動しているものもxyz平面に射影してやれば正弦波状の解ができます。これは許される振動ということになります。
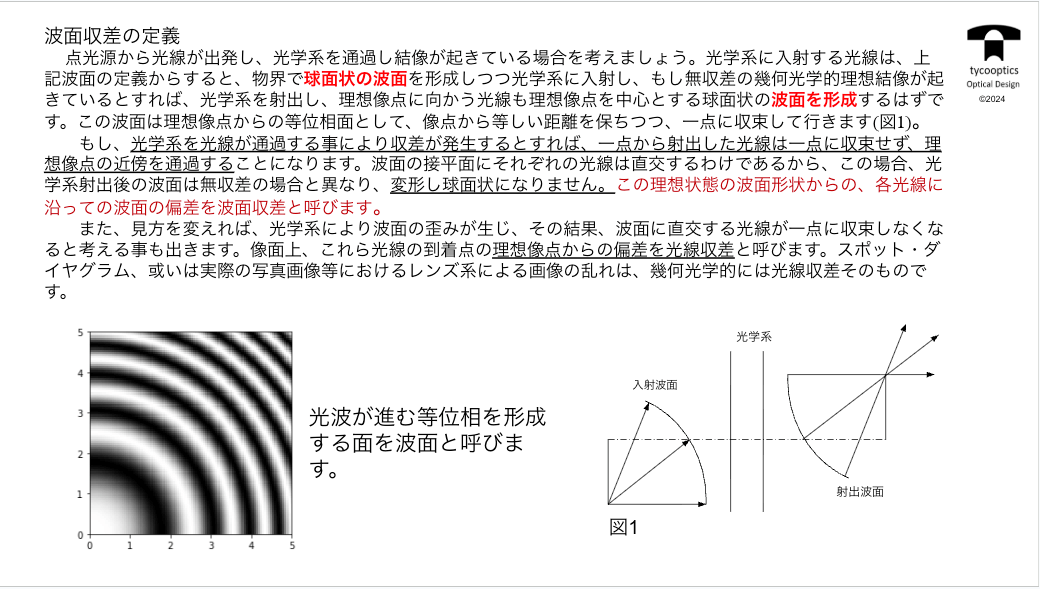
【波面収差の定義】
ここからちょっと新しいところですが、波面収差というのを定義しなければいけません
波面収差は波動光学を考える場合には非常に重要で、レーザービームを考える場合にも波面という概念が非常に重要です。
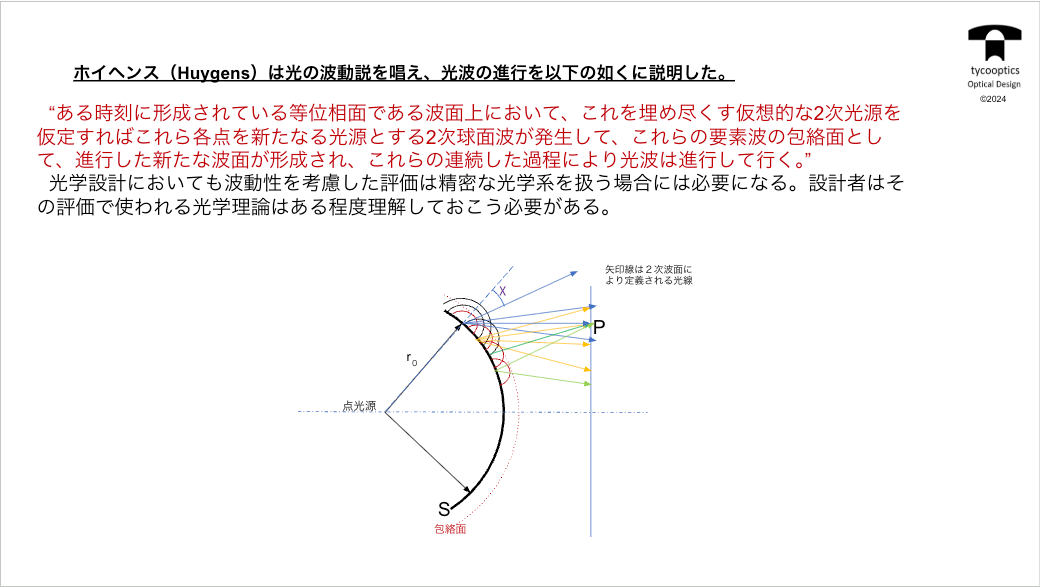
【ホイヘンスの原理】
リアル波面と最小波面の差が波面収差になってるということが重要になってきます。
この波面収差によって、実はこれからやる波動工学的な計算に意味を持ってくるということになります。
ここで話に戻りまして、ホイヘンスの原理というのは、これはですねホイヘンスの1678年、ホイヘンスが波動論、もちろんこれニュートンの粒子説とか波動説ともめてるころです。
ホイヘンスの波動説は光が解説したり干渉したりってのはうまいこと説明できますが、光がまっすぐ進むという意外と単純なことが説明しづらかったわけです。
これをどう説明するかというので考えたのが、このホイヘンスの原理です。
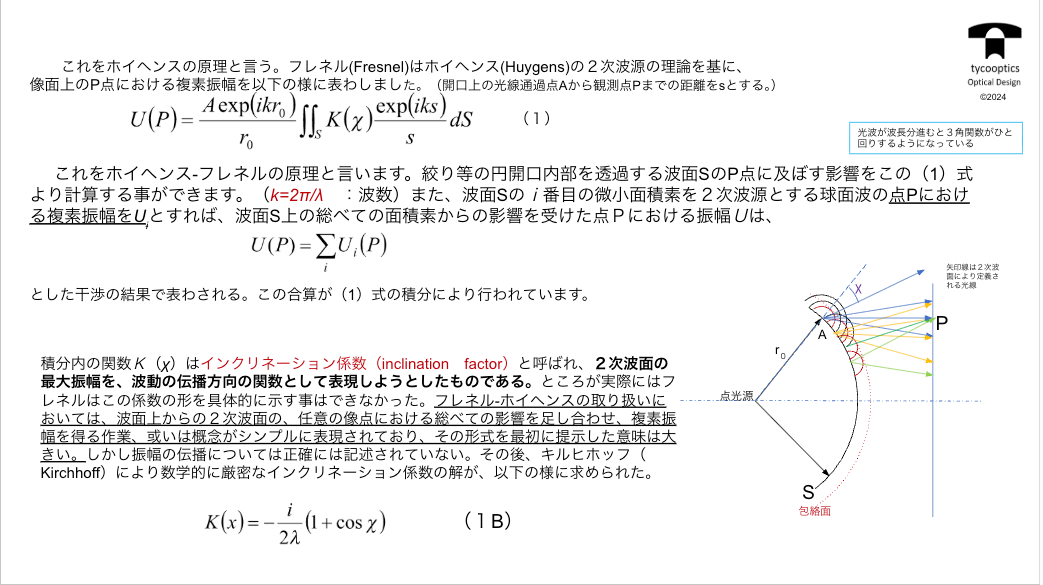
【フレネルによる定式】
無数のこの連続的に存在する2次波面からのTまでの光、具体的には位相、距離を測ることによって位相が分かります。
その合計によってここの明るさがわかるということです。
これが実はこれを定式化したのがフレネルです。
【インクリネーション係数】
ホイヘンス-フレネルの原理の際に出てくるKというものがインクリネーション係数、インクリネーションファクター、傾斜係数です。
【付録:フラウンホーファー回折近似式の導出】
これは付録で付けました。時間があれば見ていただきたいです。
これまでの厳密な積分を、フラウンホーファー回折近似というのでやって分かりやすくしたものです。
【振幅と強度の関係】
前トピックに引き続き、振幅と強度について話していきます。
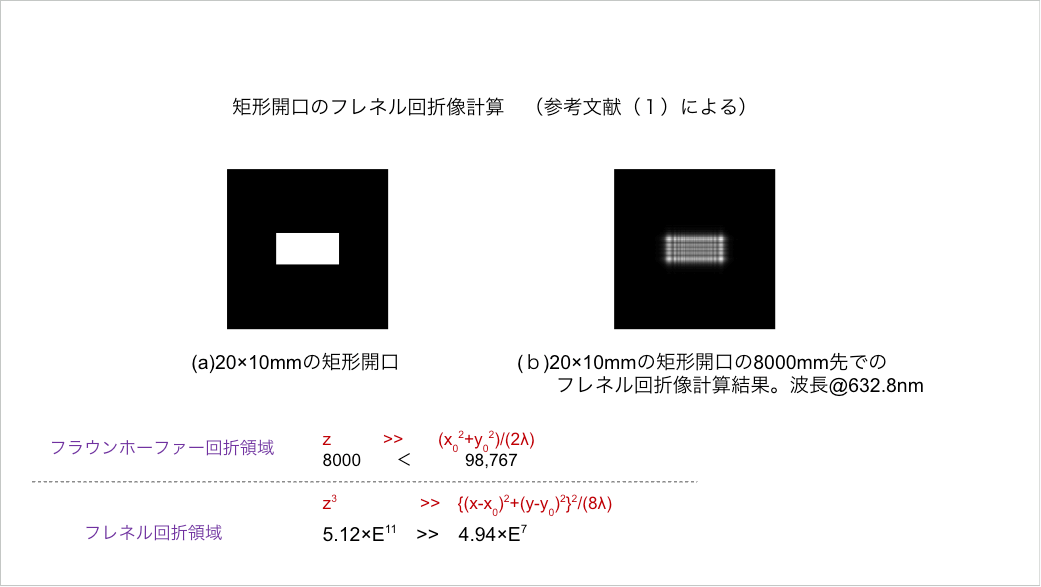
【矩形開口のフレネル回折像計算】
さっきのフラウンホーファー回折像はもちろん谷田貝先生のプログラムで計算できるのですが、フレネル回折計算、もうちょっと精度が高くなきゃいけないやつも計算できます。
10×20㎜っての円形開口の場合、これを8000㎜先で見たらどう見えるかということです。8000ミリも先だからフラウンホーファー回折像でいいんじゃないのかって思いますが、実はフレネル解説像計算じゃないとダメなんです。
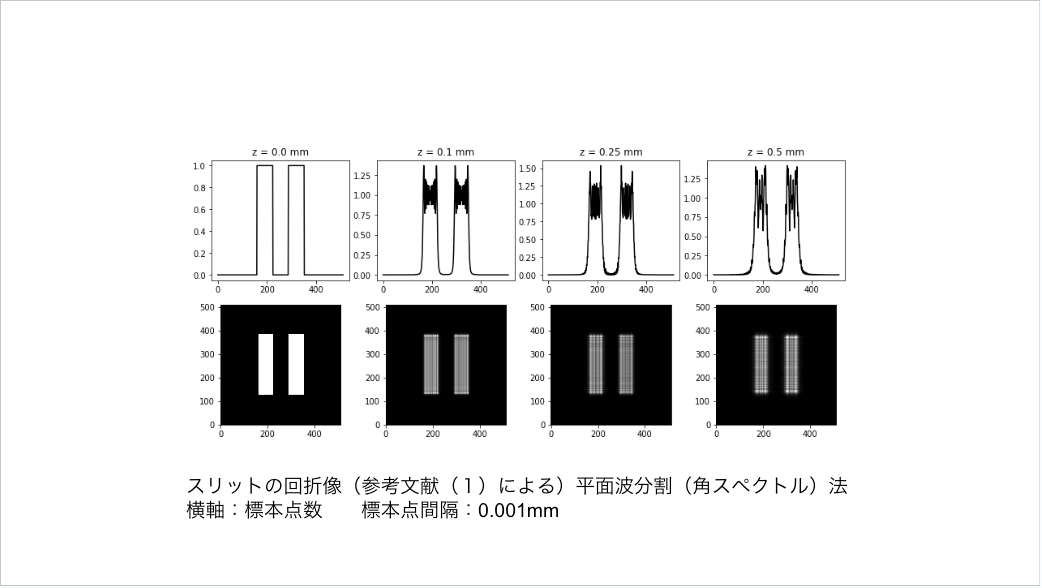
【付録:平面波分割(角スペクトル)法の考え方】
平面波分割角スペクトル法についての解説です。皆さんレーザービームの設計されるときには、現状光学設計ソフトっていうのを使わざるを得なくなってきてるわけですが、その場合もちろんフレネル回折とかフラウンホーファー回折でもできるんですけども、この平面波分割法でやると精度を気にすることなく計算できるので、圧倒的にこの手法でやれてる場合が多いわけです。
【無収差レンズの回折限界】
フレネル回折像はものすごく遠くじゃないと観察できないっていうことになってしまいますよね。
例えば20×10㎜の絞りで、リアルな絞りではそんな大きいものではないので、
8000㎜先でもフラウンホーファー回折像は観察できないということになってしまいます。
しかし、1㎜の絞りの手前にレンズを付けてやれば光が収束し、そこの収束した先にはミニフラウンホーファー回折像が形成されることになります。
【レーリーの限界】
レイリーの限界とは、レイリーという人が、どのくらいまで2点が接近した時に分解できるかっていうのを考えたものです。
レイリーの限界というのは一つの目安になります。
【ガウスビームの伝播】
ガウスビームとはどういうものでしょうか。
皆さんご存じの通り、今のところだいたいトップハットという、絞りに光が入るときに全部その絞りの中でビームの強さが均一なものを大体想定してたわけです。
普通のインコヒーレントというのはビームを形成しづらいんで、そういう状態が一般的なのですが特にガウスビームで顕著なのは独特の中央部が高い形になります。
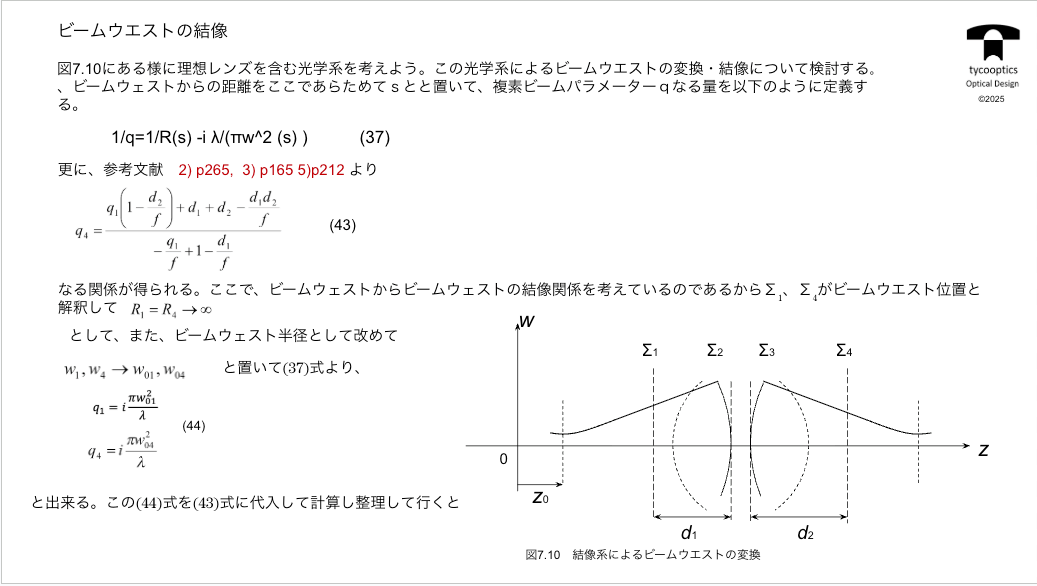
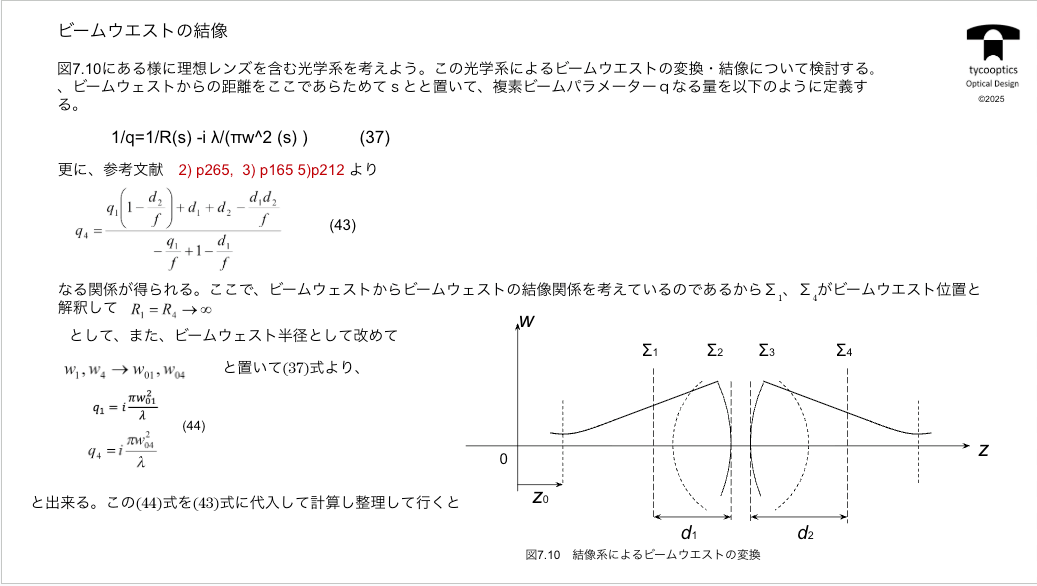
【ビームウエストの結像】
今度はビームウエストがどこにできるのかという計算をここでやっていきます。
コゲルニクという人はビームのウエストや直立半径を一緒に表すために、複素ビームパラメーターqっていうものを考えました。これは何かというと、複素数である意味は結局はハドメエクスポネンシャル表示と同じで虚数と実数によって2つの変数を格納できるという便利さ。
それから演算もこれで可能になるという便利さということになります。
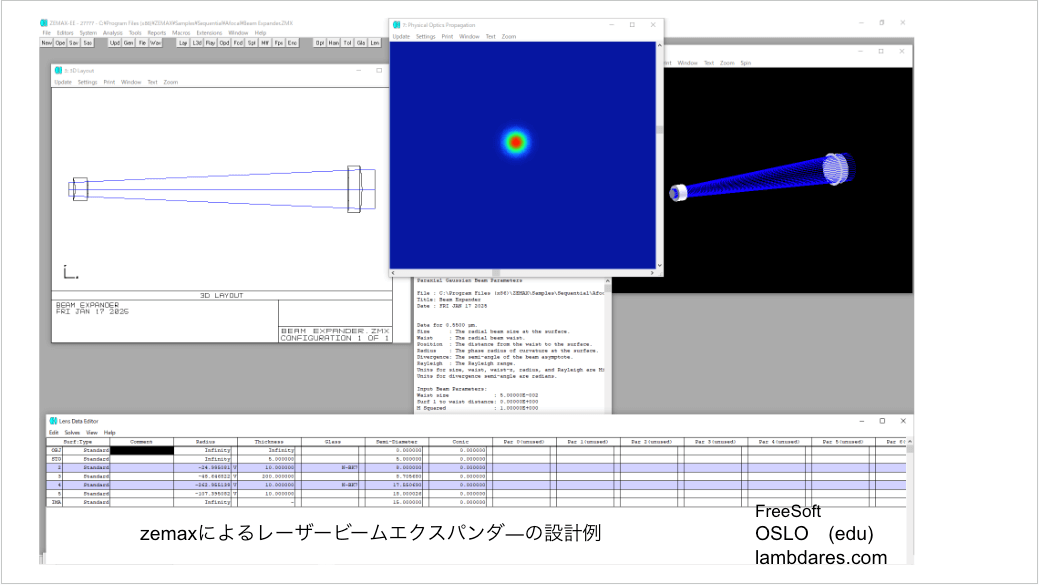
【zemaxによるレーザービームエクスパンダーの設計例】
zemaxというソフトでビームの計算をやっている例の解説です。
【4群アフォーカル系】
ビームエクスパンダーの話が出たので、ここでその話もしていきます。
ビームレーザー系は収束してる場合には結構様々な使い方があるので一概には言えないですが、ビーム、太さを変更するという形が結構多いかなと思います。それについてちょっと最後お話しさせていただきます。
講義余談
結像性能評価MTFと像の明るさについて:Fナンバー、周辺光量
【はじめに】
ガウスビームの伝播について前回、補足でやらせていただいたんですけれど、それについてちょっと言い足りないところがございました。
復習を兼ねて補足させていただきたいと思います。
【ガウスビームの伝播 補足】
これまでの光線追跡と違う式が出ています。これは手っ取り早く言うと、ガウスビームのような光が入ったときに、中央部が高くて周辺が緩い分布のビーム、あるいはフレネル数といいまして、ビームウエストが非常に小さいところから、かなり遠方のところまで強度を、明るさを計算したり、遠くでビームを受けたりする場合に、計算の、低フレネル数になって、特殊な波動光学的な状態になるということです。
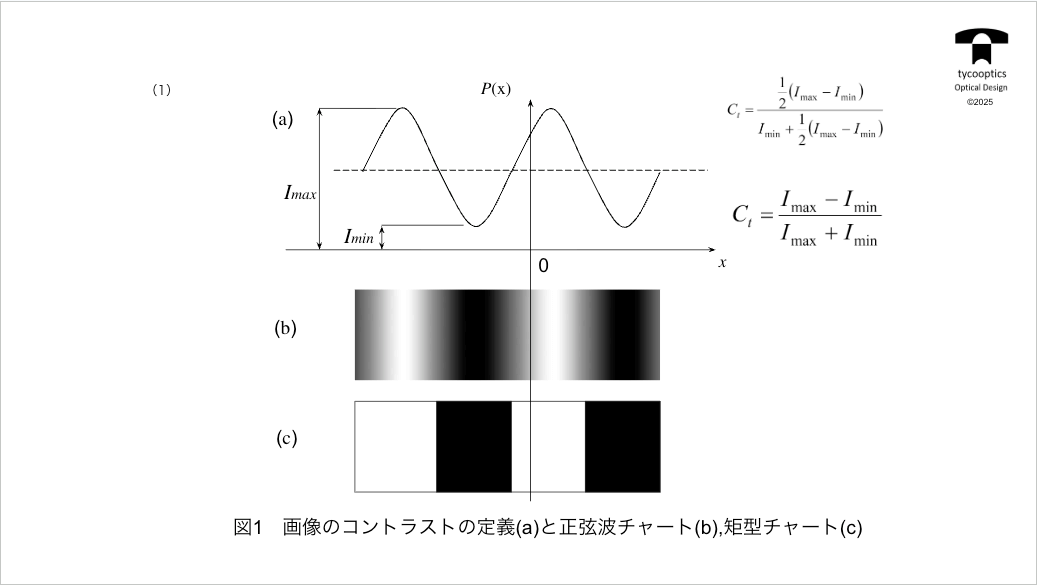
【画像のコントラストの定義と正弦波チャート、矩形チャート】
ここの白と黒のボヤッとしたところ、これをどうやって表現しようかということで、こういう模式を考えました。
【フーリエ変換の原理】
こういう正弦格子のような関数があるとします。これをですね、まず近似してみようと。正弦波の足し合わせによって周波数が整数倍の正弦波を何個も出してきて、この正弦格子のような関数に近いものが再現できるかという、実験ですね。
【OTF,MTF,PTFの関係】
もうちょっと厳密に定義すると、フーリエ変換の式というのは定型的なものですけど、それをバックグラウンドのもので割って定義するという、これが、Optical Transfer Functionというものの定義でございます。
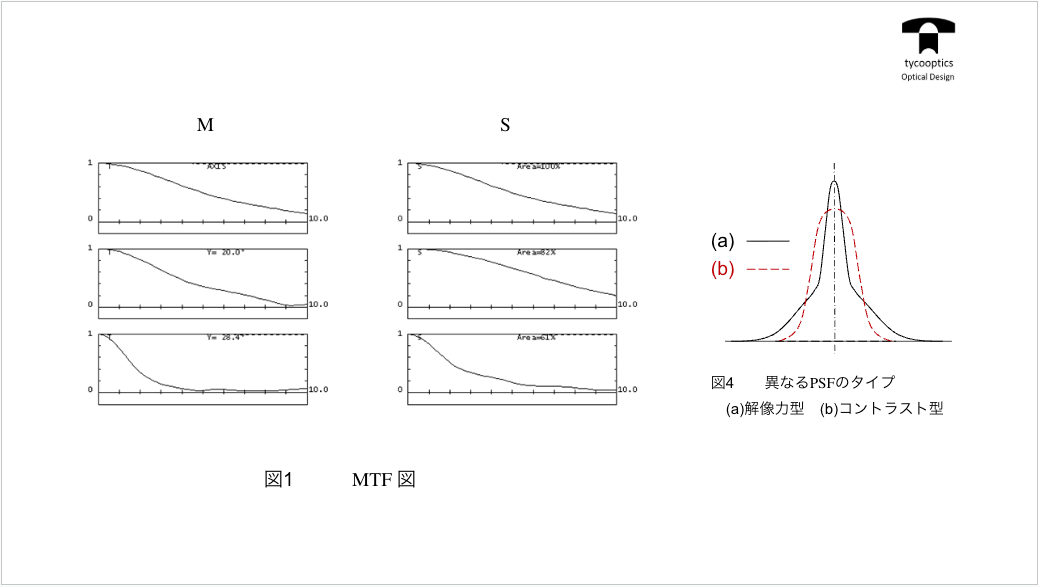
【MTF計算に用いた光学系のスポットダイヤグラム】
Point Spread Functionって、一点からでて、何百という光を集光させて、このように広がりますよという、これをまあいわば、ドットの情報なんですけど、連続的な情報とみなして強度分布とみなしてるわけですね。
【MTFの計算】
MTFって、これなんだっていう話なんですよ。一旦下がって、上がってるじゃないですか。これあの、僕らレンズ設計やってる側からすると一旦下がったところまでしか読んじゃだめって言われてるんですよ。いくらコレが上がったといっても、一旦下がってしまったらこれはもう死に体なので。
【COSとI(x)の積】
実際にコンピューターの中でやってることですけども、強度分布に知りたい周波数のコサインをかけてやることでMTFが計算できるんですね。
【低周波数MTF、そしてPTFの影響】
これはX線写真なんかで考えられる方法なんですけど、独特な考え方でして、X線の明るいところと暗いところで、収差があってグラフ線が鈍くなります。そうすると本来あるエッジのグラフとの隙間に面積が生じます。この面積が小さければ小さいほど、当然先鋭な絵ができてるということになります。
【絞りに関する復習】
像の明るさ、照明関係の話です。これまでFナンバーということで像の明るさについて触れさせていただいたんですけど、これからもう少し詳しくお話させていただきます。
【ビグネティング】
もう一つ画面の明るさについて重要なのは、青い光が実は、絞りをいっぱい通っていないんですね、赤でもそうなんですけど、絞りから浮いてしまってるんですね。コレなぜかって言うと最終レンズで引っかかってるんですね。
【色度座標】
光を明るさで捉えていこうということで、人間の目ってどういう感度があるかって言うと、400~700くらいの帯域に感度があります。青いあたりが一番ピークが高いということで、赤や紫に比べて何倍も感度があるということになりますね。ですからここらへんは光学設計でも主波長ということになります。
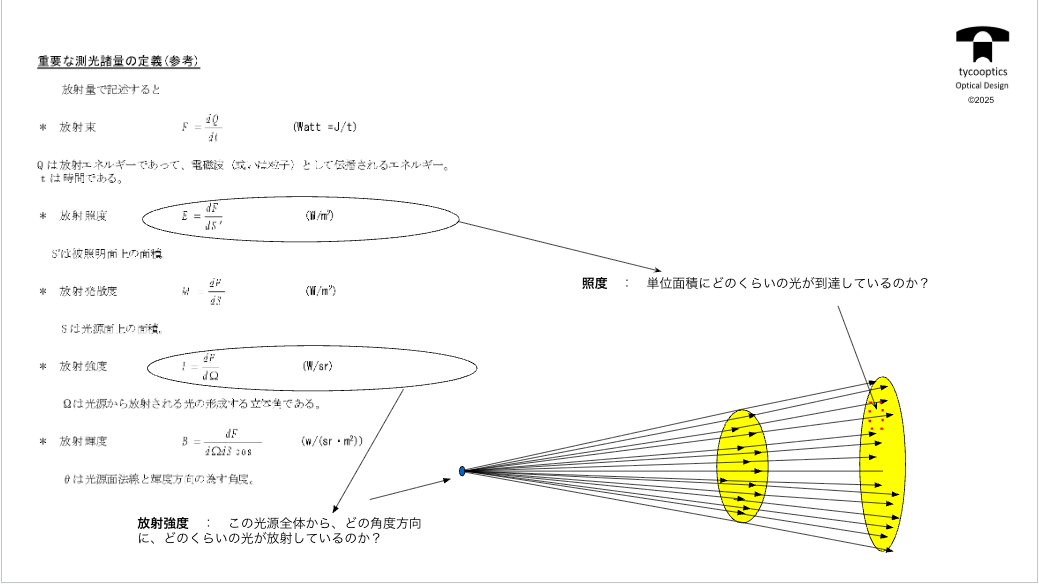
【重要な測光諸量の定義】
これは測光学なんですけど、一応定義しておきます。
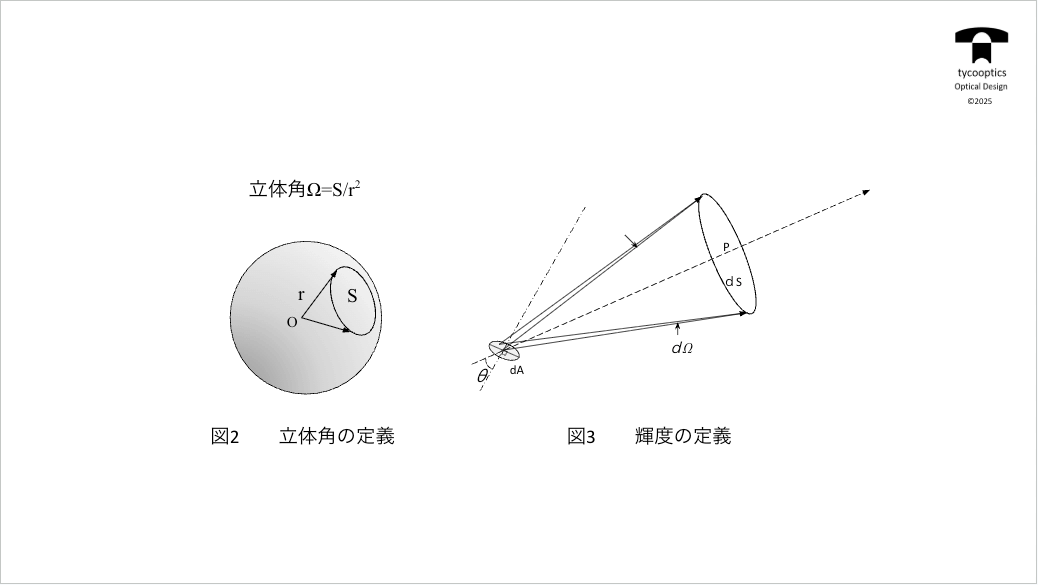
時間あたりの明るさ、エネルギー、ワットのことを放射束と呼び、像の明るさを表現するのを放射照度と呼び、単位面積からどのくらいのエネルギーが出てるかのことを放射発散度、単位立体角あたりにどのくらいのエネルギーが出ているかのことを放射強度、単位面積あたりに放射されるエネルギーのことを放射輝度と呼びます。
【照明単位系(放射量、測光量)】
測光量というのは標準比視感度をかけこんだものです。
【Fナンバーとはなんだったのか】
これももうお話しているんですけれども、Fナンバーってじゃあ一体何だったのかっていうお話ですね。この測光量の概念が頭に入っているとよりわかりやすくなるかなと思います。
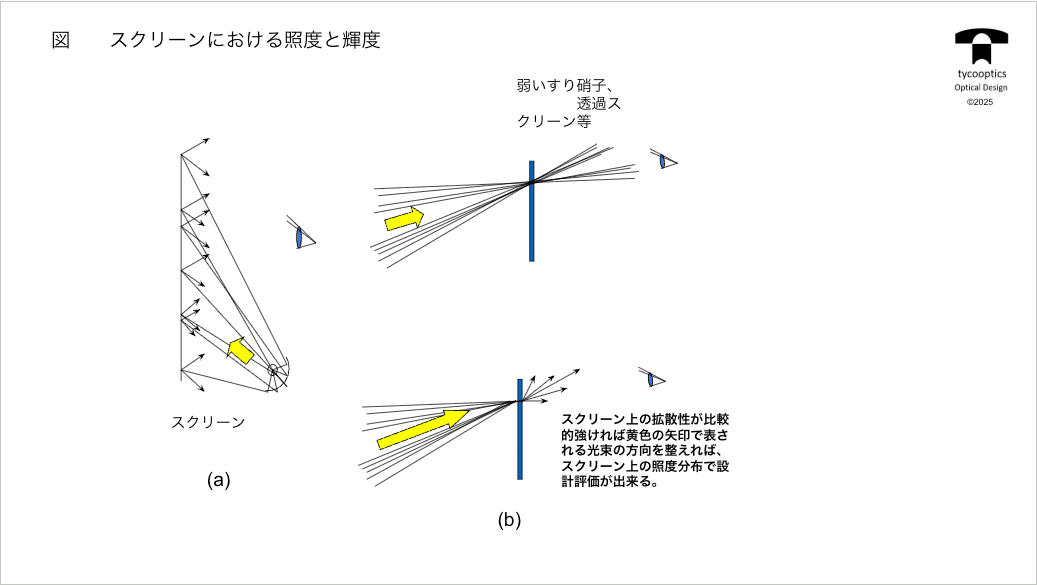
【スクリーンにおける照度と輝度】
測光量のお話なんですけれども、どういうふうに使い分けるかということですね。
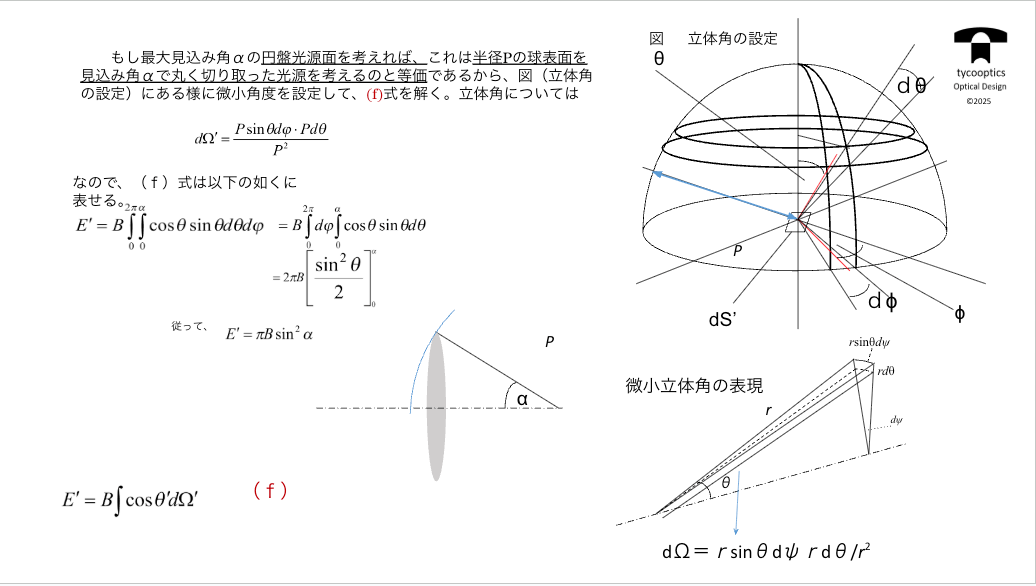
【立体角の定義 輝度の定義】
立体角ってさっきから申し上げてますが、これはすべての物理の分野で重要なことなんですが、一応申し上げておきます。
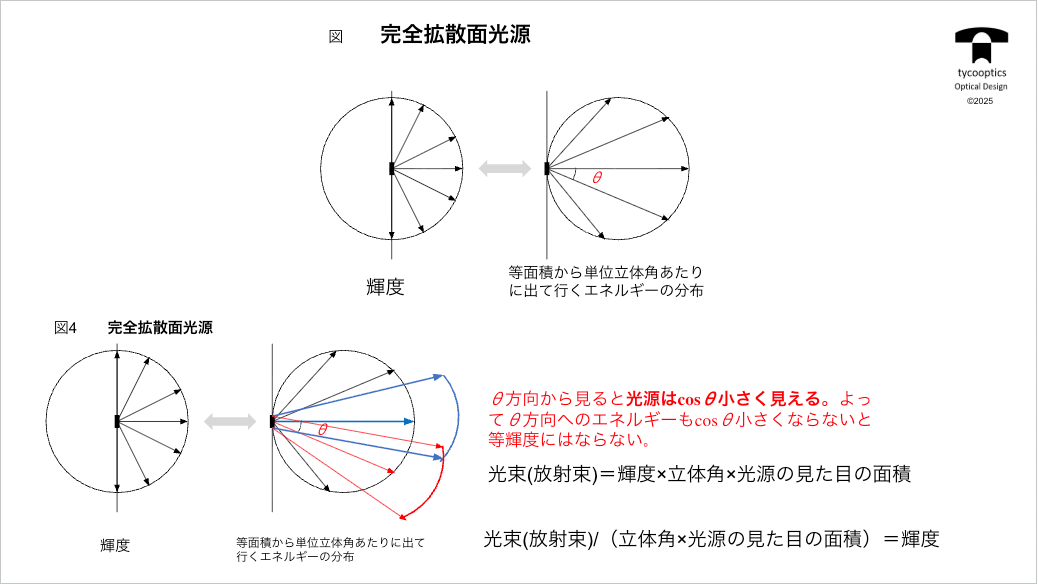
【完全拡散面光源】
照明系の話で完全拡散面光源、ランバーシアンというんですけど、これを定義する必要があります。
【周辺光量の考察】
Fナンバーというのは、画面中心の明るさのことですね。コレ今有限距離があるんでFナンバーじゃないんですけど点光源が無限遠に合った場合にはこれがFナンバーです。
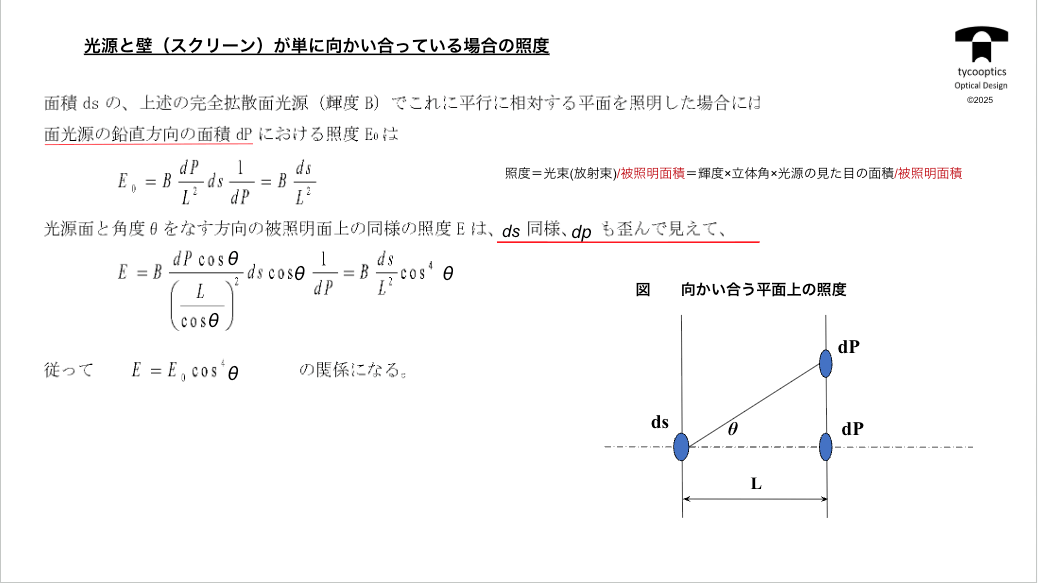
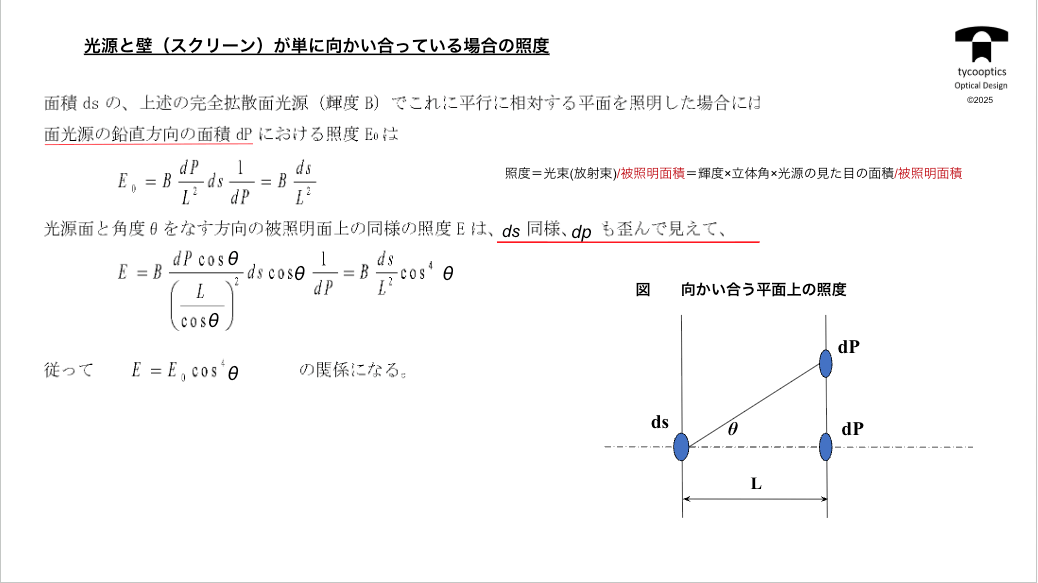
【光源と壁(スクリーン)が単に向かい合っている場合の照度】
コサイン4乗則の重要なことです。例えばレンズがない場合、ここの壁にdsっていう光源があって、コレが真正面に壁が合った場合に、ここの壁の中央と周辺でどれくらい明るさが違うか、ちょうどコレのレンズがないだけのパターンですね。
【質疑応答】
照明系光学設計について
【照明系光学設計とは】
本来は最適化というのが10回のテーマだったんですけど、前回結像系の像の明るさについてお話させていただいて、その時の続きでもう照明系光学設計というカテゴリーの話をさせていただきます。
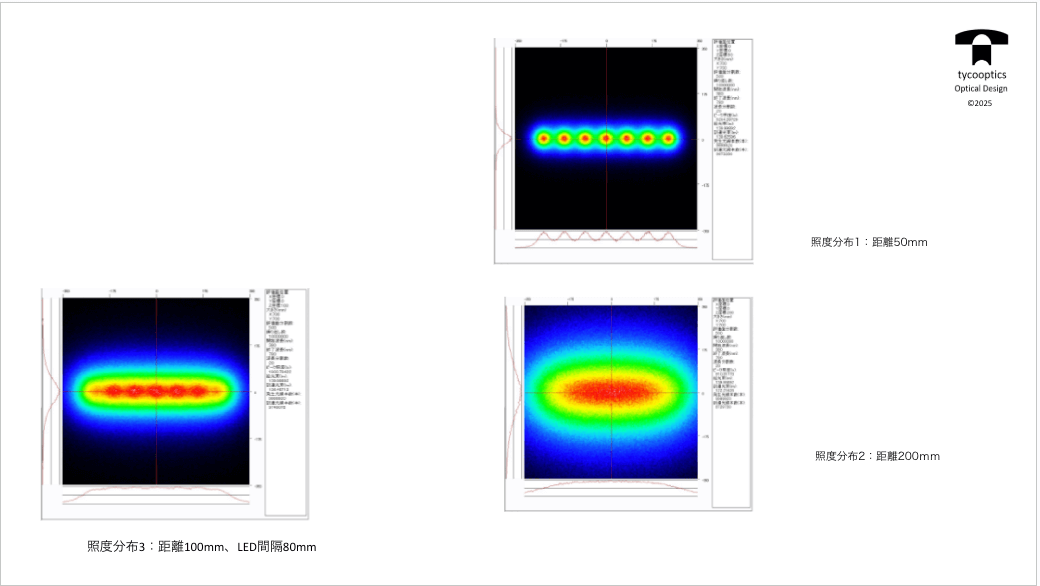
【照度分布】
ソフトで計算しますと、どこの距離で、この距離を離すときと近いところで当然、ここの離れ方が変わり、分布も変わってきます。
【面上の輝度分布】
じゃあこのときですね、光源から出てる輝度分布を測ってみようと思います。このソフトで照度分布を測ります。
【拡散シート】
LEDを使って並べるという方法を取っている限りは、拡散シートを入れて、光を拡散させるか、あるいはアクリルの四角の直方体みたいなのをいれて、その中で光を何回も反射させて導光板と言えるようなものを形成して、光をぐちゃぐちゃにして、ある意味拡散させるか、
【レンズ拡散板表面構造】
どんな構造になってるかというと、拡大してみるとこの様になっています。凹凸がいっぱいあって、レンズ的な役割をしています。
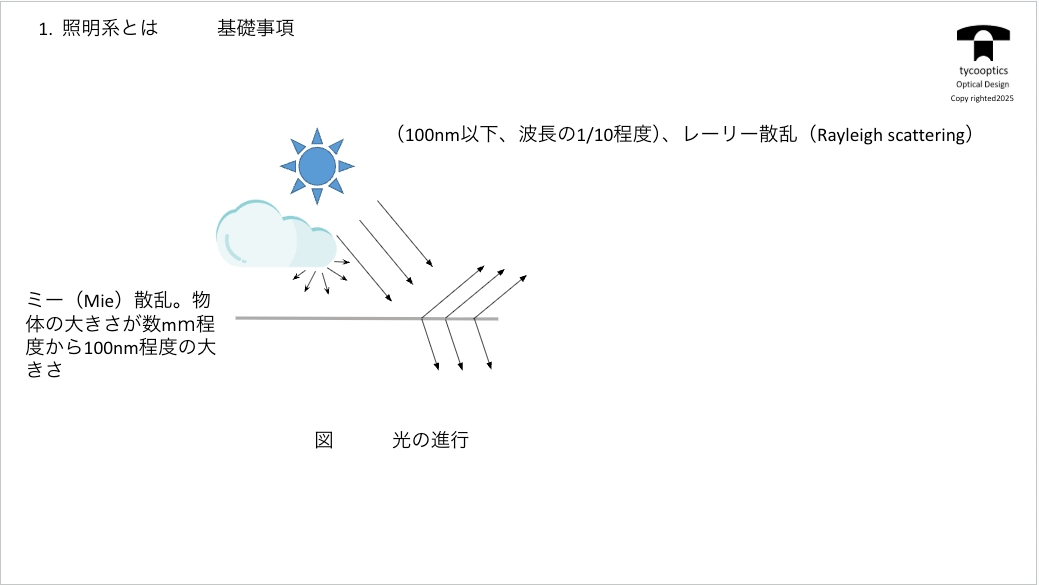
【照明系とは:基本事項】
ここからは正式な照明系の、測光学の入門ということになります。
【測光学】
光の明るさを考えようというのは測光学という単位、コレは前回お話しています。簡単に言うと、光束や光度。物理量で言うと放射強度、輝度など、代表的な単位となります。
【スクリーンにおける照度と輝度】
コレも前回お話したかな、スクリーンもやはり拡散性が非常に重要だというお話です。
【輝度の測定原理】
コレ実は、輝度測定機なんですね。輝度測定機って実際にはどのように測っているかというとですね、もちろんこれ実際に運用しやすいように色々工夫は凝らされていますけど、一番カンタンに考えるとですね、写真で撮ってるんですね。
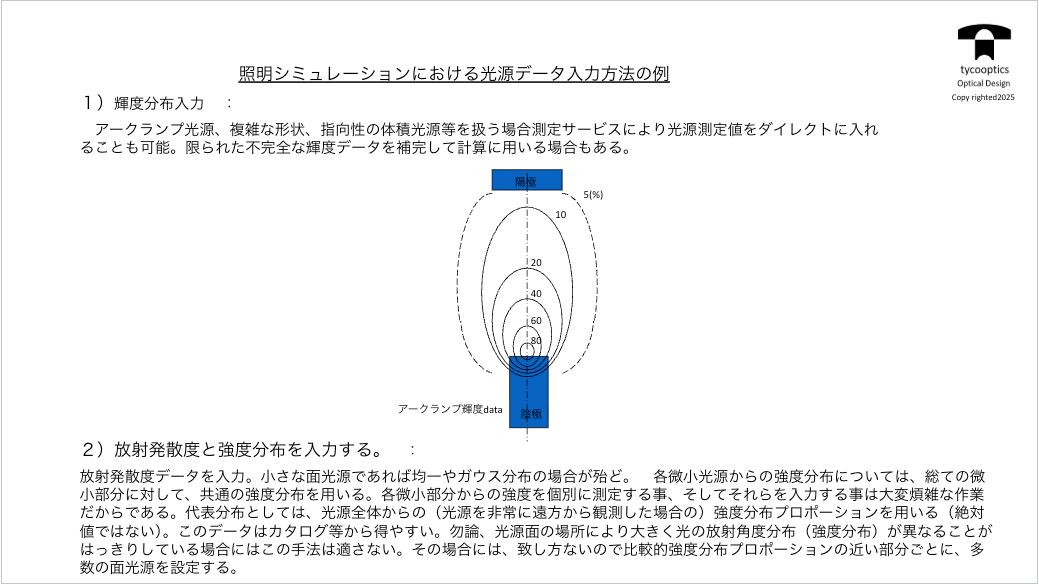
【照明シミュレーションにおける光源データ入力方法の例】
あとはですね、かなり本当に照明系設計の話になるんですけど、光源というのは面が光っているものばかりではないんですね。アークランプのようなものは空間が光ってるんですね。
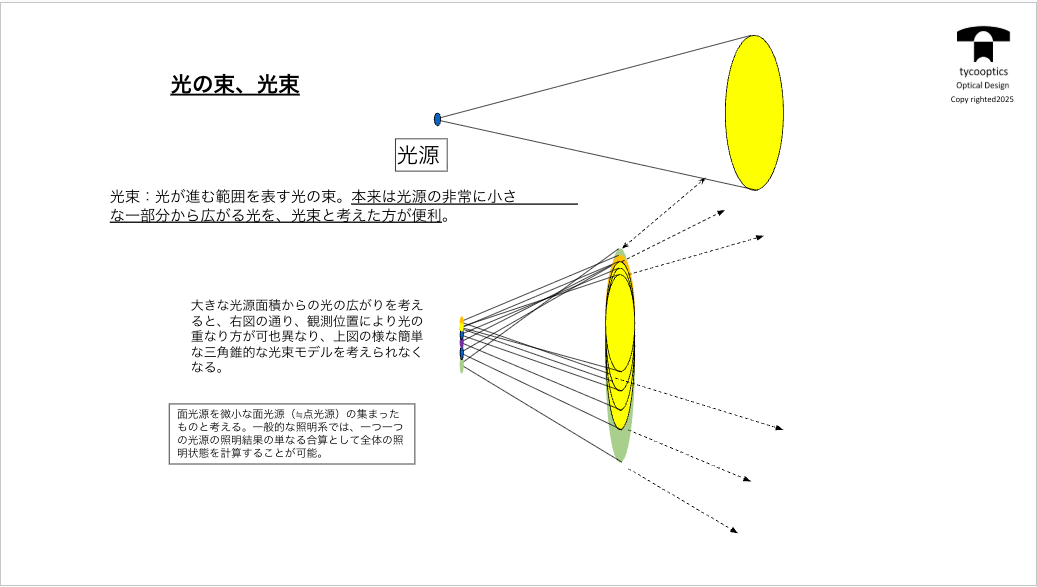
【光の束、光束】
先ほどの輝度分布を光源データとして使えれば一番いいんですけど、実際にか輝度分布がわからなかったり、入れるのが大変だったりするので、このような感覚で入れる方法があります。
【照明系設計の簡単な法則① 輝度不変則の概念】
輝度の不変則というお話をいたしましたが、これはちょっと皆さん気になると思うんですが、例えばすごく遠いところで、眩しいライトをこっちに向けている。眩しいですよね。これが輝度不変なんですね。
【航空管制塔の例】
LEDっていうのは、輝度が低いですよね。例えば、航空管制塔みたいなものがありますよね。
【照明系設計の簡単な法則② 放射照度の余弦則】
細かい話ですけれども、照明系計算の簡単な法則。これ幾何光学の収差論と違って、数式的には非常にシンプルなものしかないんですね。
【照明系設計の簡単な法則③ 光錐体の定理】
ここはちょっと細かい話なんですけど実際にはもうこの、立体角、ちょっとめんどくさく見えますけどこれ、非常に単純な話なので、この測光学を考えるときの定番なんですよね。
【微小立体角の表現】
これを、面光源が光ってるとして、光がどう飛んでるか、コレ立体角の条件なんで、これ定番ですよね。
【瞳のマッチング フィールドレンズとテレセントリック系による】
コレ難しくないんで、じっくり見ていただければわかるんですけどここで大事なのは斜めになった分だけコサインシータ分だけ暗くなることですね。
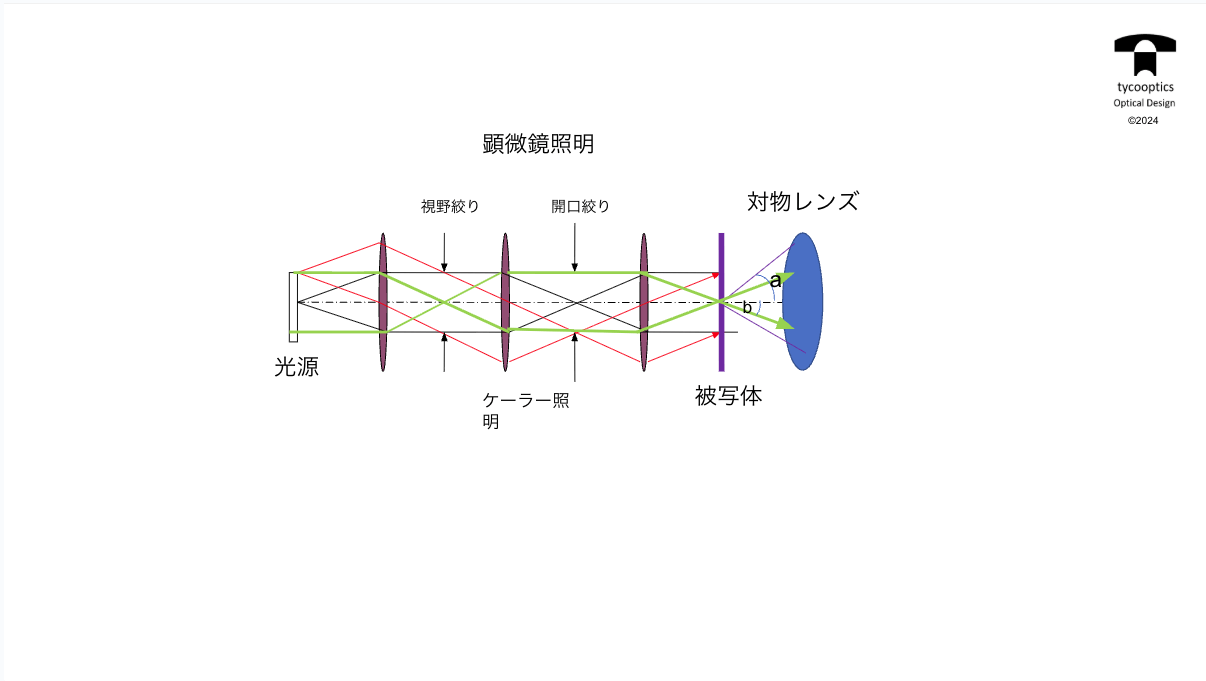
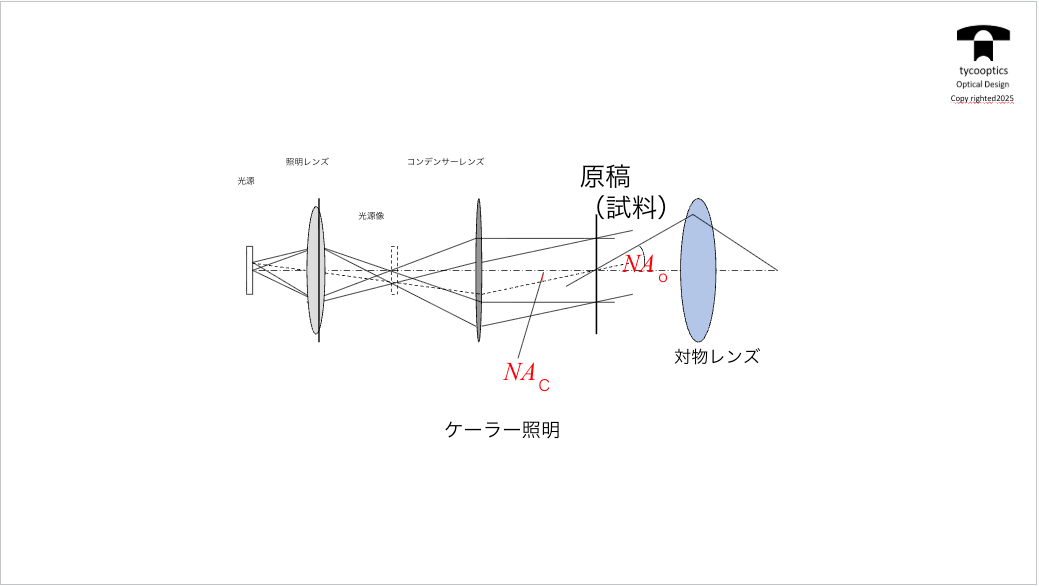
【照明系の基本的パターン ケーラー照明とクリティカル照明】
照明系っていうのは結局ですね、被写体を照らすということなんですけど、基本的に2つのタイプがあると思っていただいて間違いないかなと思います。
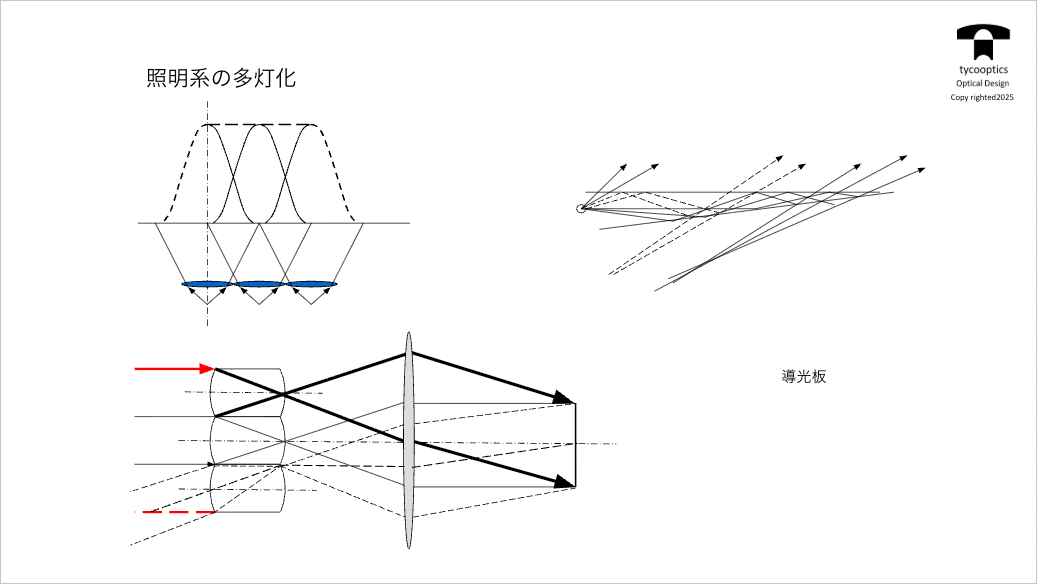
【照明系の多灯化】
照明系はこの2つだけでできている訳では無いので、これを多灯化するというバリエーションになってきます。
【フライアイレンズの概要】
高級なフライアイレンズっていうのは一個一個研磨して別々に作ってるんですね。それを柱状に切って重ねてるという非常に精度の高い加工をされています。
【バックライト照明系の構造】
さっきのバックライト照明も詳しく説明します。光源がありまして、導光板も真ん中に入ってまして、導光板から抜けるやつをまた再び上げてくるための反射板っていうのが底についてます。
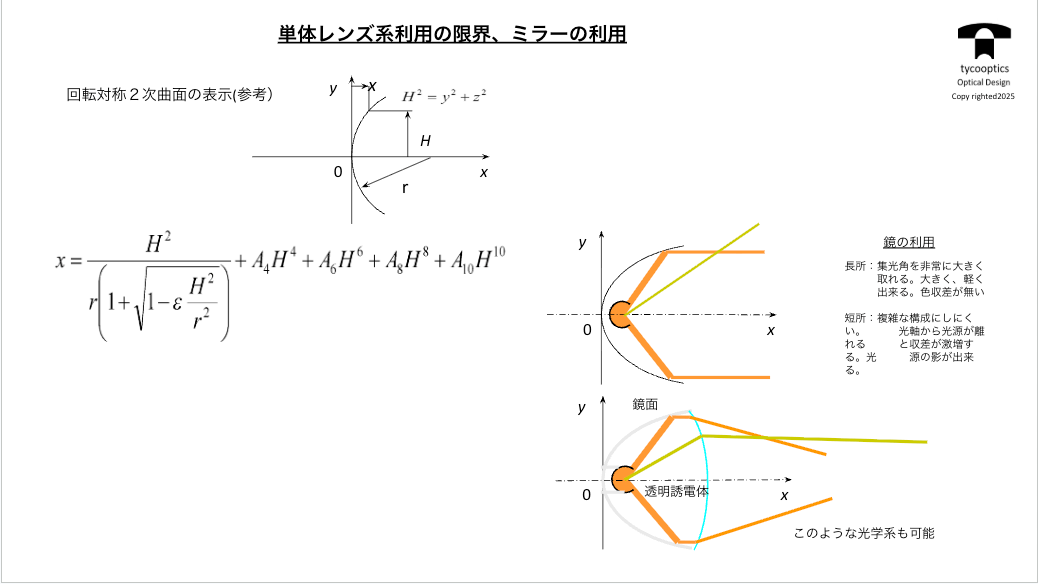
【単体レンズ系利用の限界、ミラーの利用】
レンズっていうのはですね光の取り込みの限界がありますよね。光源に相対して面をおいて、そこに貼る立体角しか光線が取れないので、すごく利用効率を上げようとするとミラーを使うしかないんですね。
【格子構造反射素子の断面】
照明系の蛍光灯なんかにこんなのありますけど反射板を置いといてですね広がっていく光を中に入れる巧みにできたものです。
【暗視野照明 明視野照明 共焦点顕微鏡の原理】
代表的なものは顕微鏡。
【被検面欠陥の検出】
色々照明系の面白いものがあるよという、照明の当て方によって、今まで見えないものがみえるよというのが、いろんなことでやられています。
【ケーラー照明 補足】
ケーラー照明は結局この対物レンズのNA、Fナンバーの有限の場合の時の定義、この、像を取り込む角度の大きさですね。
【質疑応答】
照明系光学設計について part2
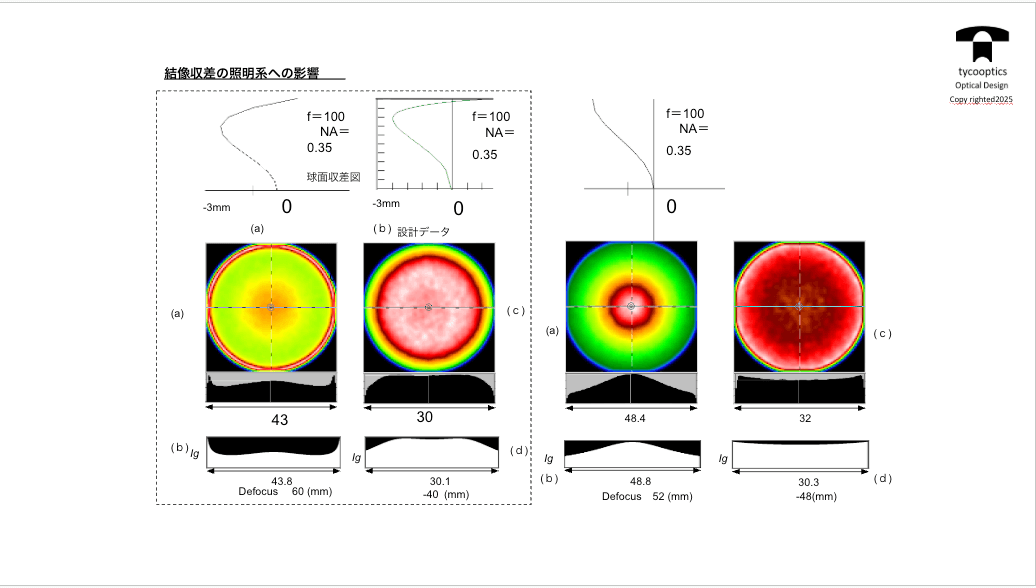
【結像収差の照明系への影響】
光のコヒーレンシーの問題でこの対物レンズの照明系を受ける光学系のNA、Fナンバーと考えてもいいですけども、それと照明系の光の開き具合の割合が解像力に微妙に影響をすると言うことを申し上げました。
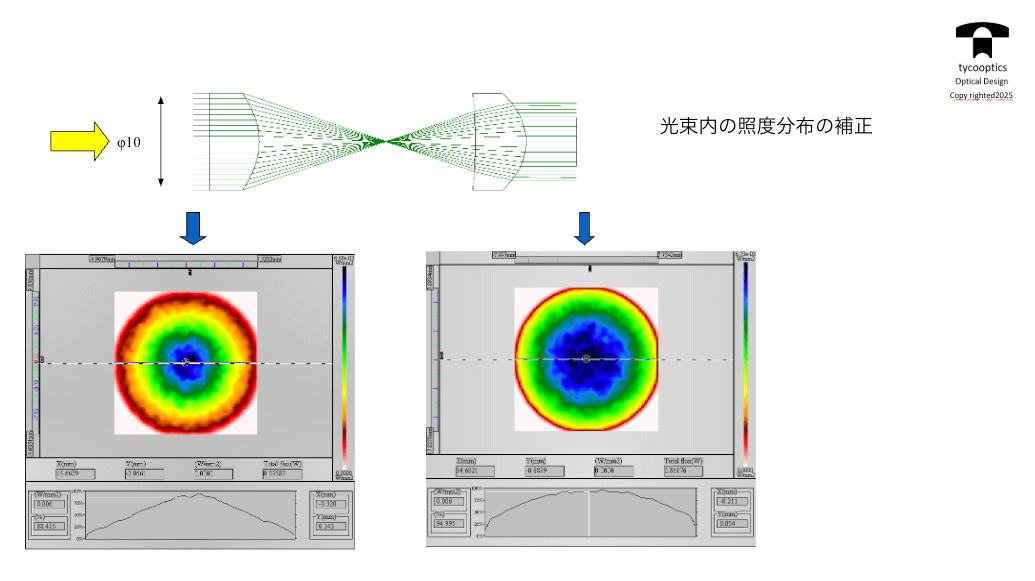
【光束内の照度分布の補正】
ガウスビームをですね、フラットにする役割を担っているレンズなんですね。これ実際に実用されてます。
【等立体角の光線の射出と入射】
例えば、点光源から光が出てると、そうすると等立体角で光線描いてるんですね。
【cos4乗則が、絞りが中心付近にある光学系については導けた】
いろんな照明系で面白いことができるよっていう話だったんですけど、ここはね今まで、コサイン4乗則って、前回結像系のお話ですけど、画面の中心、結像系の話ですね。画面の中心に比べて、一番端のところですね。このときに中心に比べてどのくらいの暗さになるか、照度がどのくらい暗くなるか。
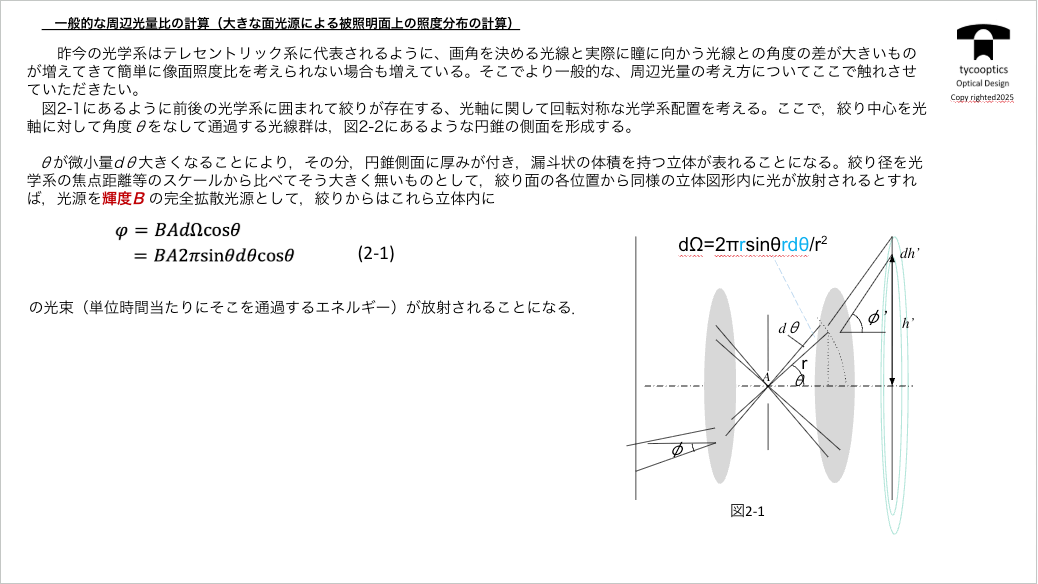
【一般的な周辺光量比の計算(大きな面光源による被照明面上の照度分布の計算)】
コレ結構ややこしい話なんですよ。測光の考え方と収差の考え方の両方ある程度覚えてないとできないんですけど、これはもう輝度に立体角を乗じてその光源を見込む角度をかけて、光源の面積をかければ、この光束内のエネルギーがわかるという、最も単純なもの、これをもとにしてるわけですね。
【絞りの前後に光学系があり、なおかつ φ≈θ≈φ’ の場合】
コレもさっきの式を利用してるだけなんですけど、
【絞りの前後に光学系がある一般的な場合】
コレが今までの日本の光学設計の教科書では答えられないんですよ。
【周辺減光が無く、歪曲収差も発生しない光学系の設計例】
絞りより前の光学系、後ろの光学系で、このシータと物体の大きさ、像の大きさが関係するような光学系を作ってやるとですね、比例関係になるんで、周辺減光が全く起きないというレンズができます。
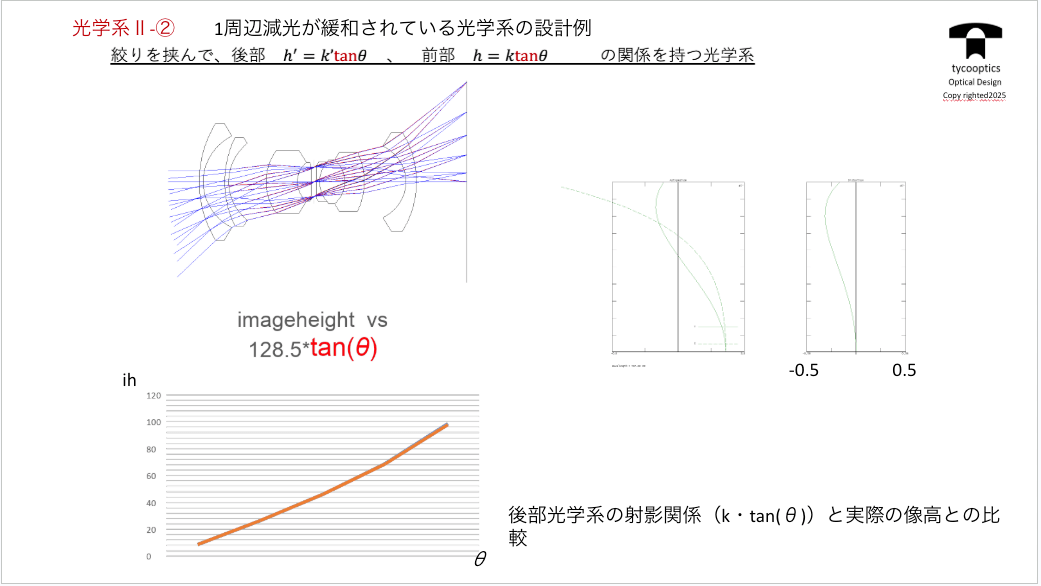
【一周辺減光が緩和されている光学系の設計例】
非常に役立つのがですね、この光学系です。コレは有名な画角の大きいレンズです。
【画角の定義】
例えばこんな光線通ってる光学系ってもちろんあるわけですよね。いろんな光線は絞りの位置によって取り方が変わります。ではこの場合画角ってどう言ったらいいのか。
【付録:絞りにおける完全拡散面光源特性の確認】
照明系では非常に面白いところです。実は解析力学はハミルトンがこの光学の理論を見たときにイメージできたという逸話があります。
【照明系設計補足:光線と熱放射線】
レーザー光源とそれ以外の光源ってちょっと照明光学的には分けて考えなくてはならない。コレが大前提です。
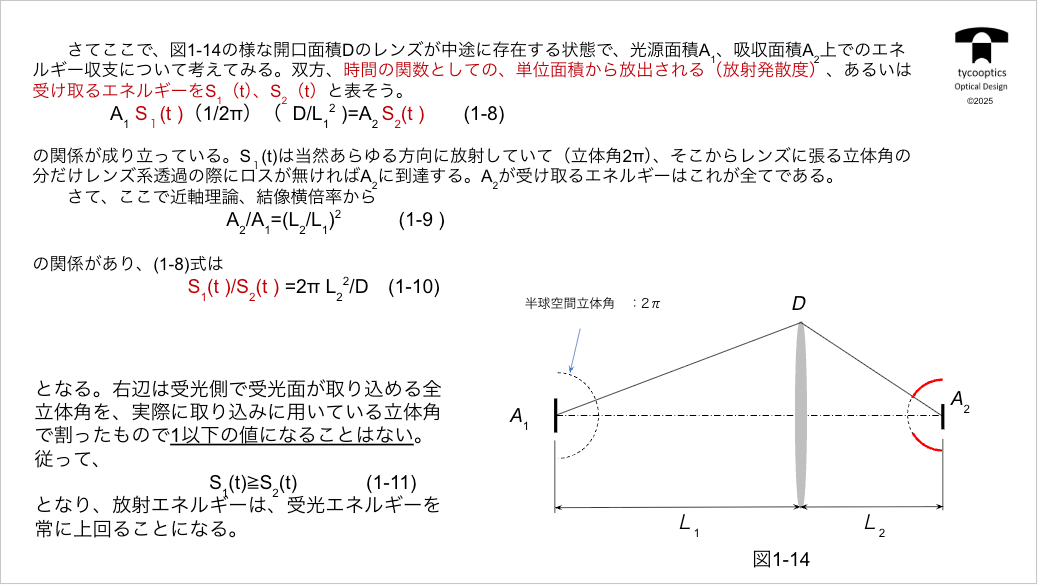
【時間の関数としての、単位面積から放出される(放射発散度)】
例えば太陽ってめちゃめちゃ熱いですよね、それをですね、レンズでですね、地球上で集光した場合、どのくらい温度が上げられるかという議論ですね。
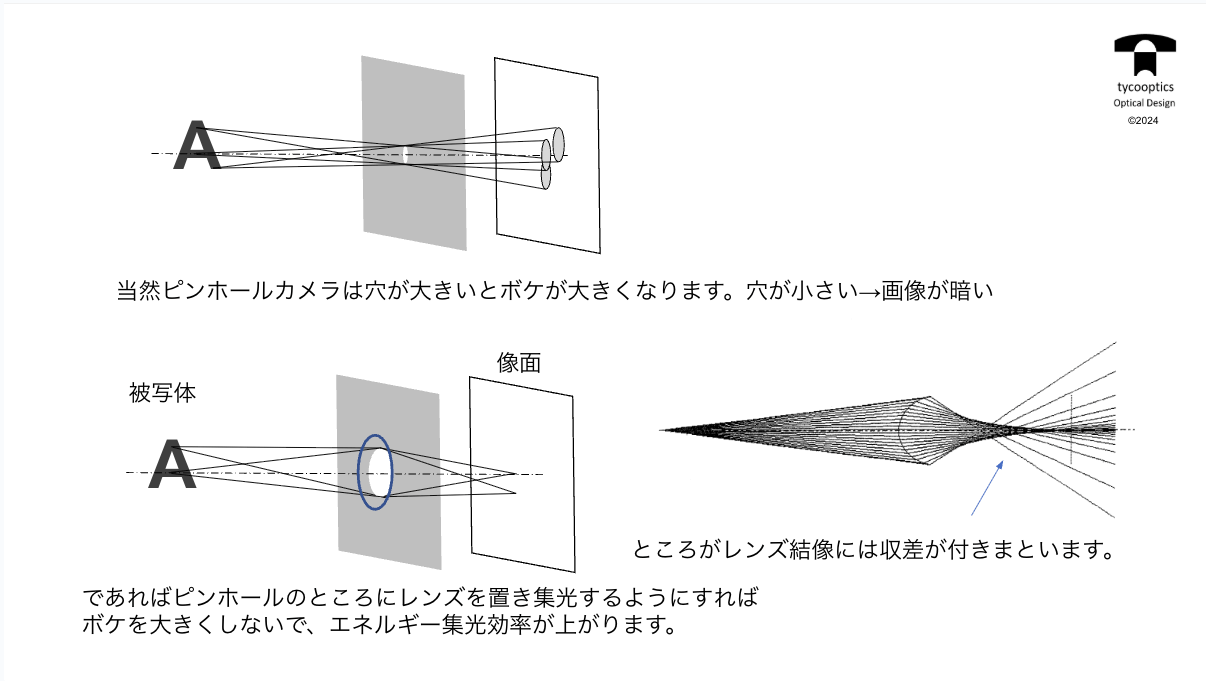
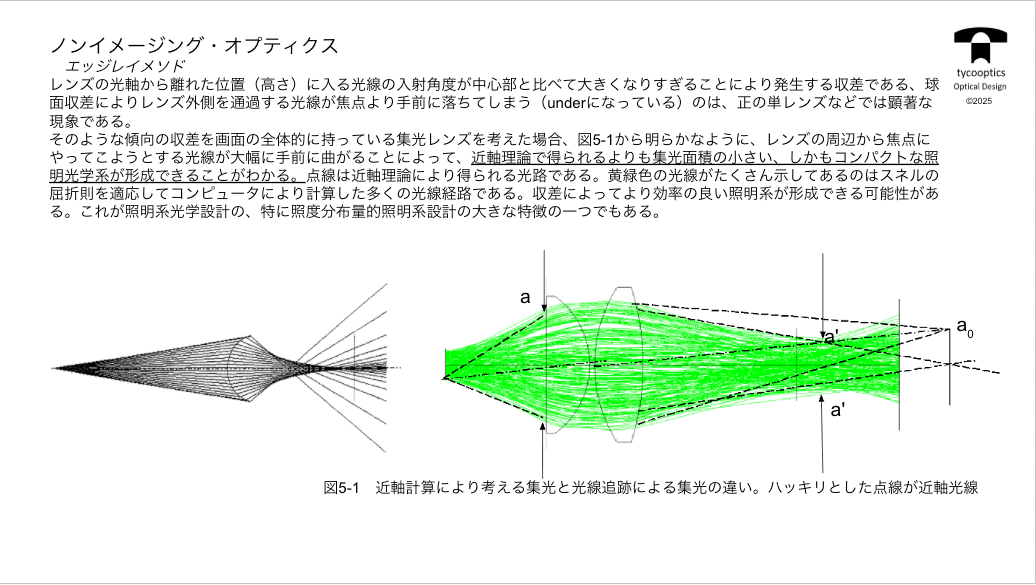
【ノンイメージ・オプティクス】
ノンイメージ・オプティクスって、名前わかりやすいですよね。光のエネルギーを取り込むってだけなんで、レンズ設計でやってたきれいな像ができるとかですね、照明系で考えても照度を均一にするとかっていう高級なものは狙ってないんですよ。
【開口と像面湾曲収差】
像面湾曲って申しましたよね。像面が曲がっちゃうんだよって、コレ別にここがでっかい像面のところがリフェクターであればですねこの穴に光をいっぱい入れればいいんで、像面湾曲なんて合っても構わないわけです。
【ライトコーン】
ライトコーンって、光をここのこっから左から光が入ってきてちょっと狭いところに集光してあげないとまさにノンイメージ・オプティクスですよね。集光密度を高めたい。コレって結構単純なように思いますよね。
【CPC(コンパウンド・パラボリック・コンセントレーター)】
コレの正解が発明されたんですね。
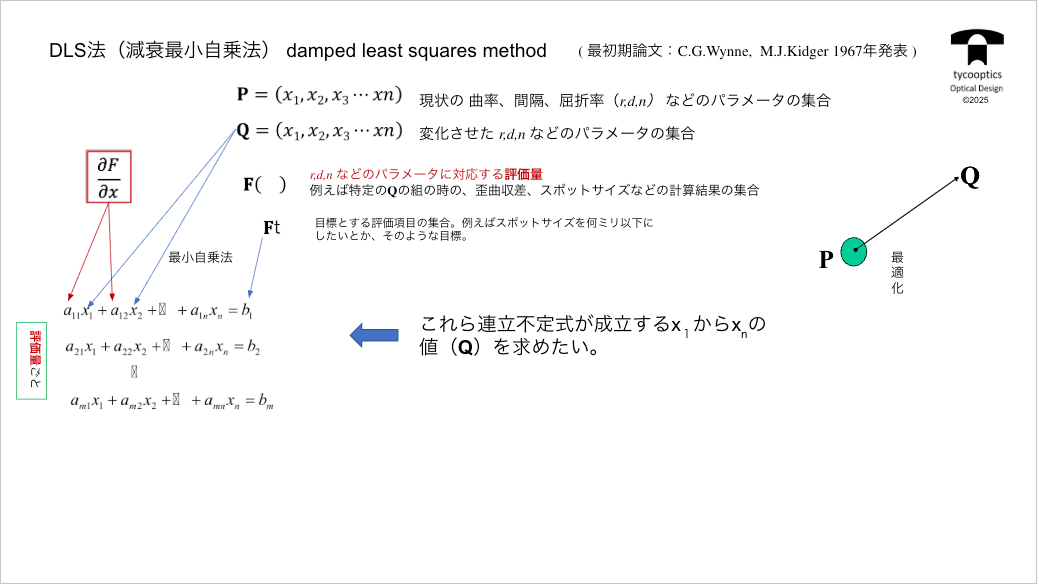
【最適化】
最適化に入らせていただきます。
【収差補正のための基本事項】
もっと前の方に収差補正についてお話させていただいていました。最適化というのは大体は収差補正に関するものなんですが、これは球面収差が少ないレンズの形というのはやりましたね。
【光学設計の流れ】
【最適化の能力】
これはですね最適化の概念っていうのはそういう感じです。単純な計算でやってるということです。
【コンピュータの最適化の際に出てくる問題】
ただこの最適化やってるとですね何が問題ってコレ直感的にわかると思うんですけど単一の評価尺度をメリットファンクションに入れるっていうのはまあ胡散臭いっていうか、一個でいいのかよっていう、まず問題があります。
【必要とされる光学設計のための能力】
光学設計としては非常に重要なところですけど、レンズ設計者という役割をこなすためにはいろんな段階の方がいらっしゃると思います。結像の構造、どうして結像してるのかは回折限界がどこだとかそういう、ある程度光学系の構造を知ってる必要があります。
【光学設計仕様】
設計の例を見ていただきたいなと思います。
【参考レンズ】
そうすると我々はですねどのくらいの構成にしようかって考えないといけないわけですよ。
【初期データ】
そうするとガウスであれば、凸レンズ、それからバルサム結合レンズ。
【ガラスの最適化と境界条件】
でまあもうあんまり良くならなくなったのでどういうことをするかっていうと、ガラスを最適化してやる。
【非球面化】
ここに一面を非球面にしてみました。一面を非球面にして最適化したわけですね。
【Global Explorerの実装】
Global Explorerはこれ、変な惑星に重力で捕まってたものを何個か、いろんな惑星を探査した結果、あしのこから、なんとか温泉くらいまで下がったって感じですかね
【質疑応答】
光学系の製造:公差/ゴースト/温度特性/光学設計の未来
【光学系の製造について】
今回は光学系の製造ということについてお話させていただきたいと思います。
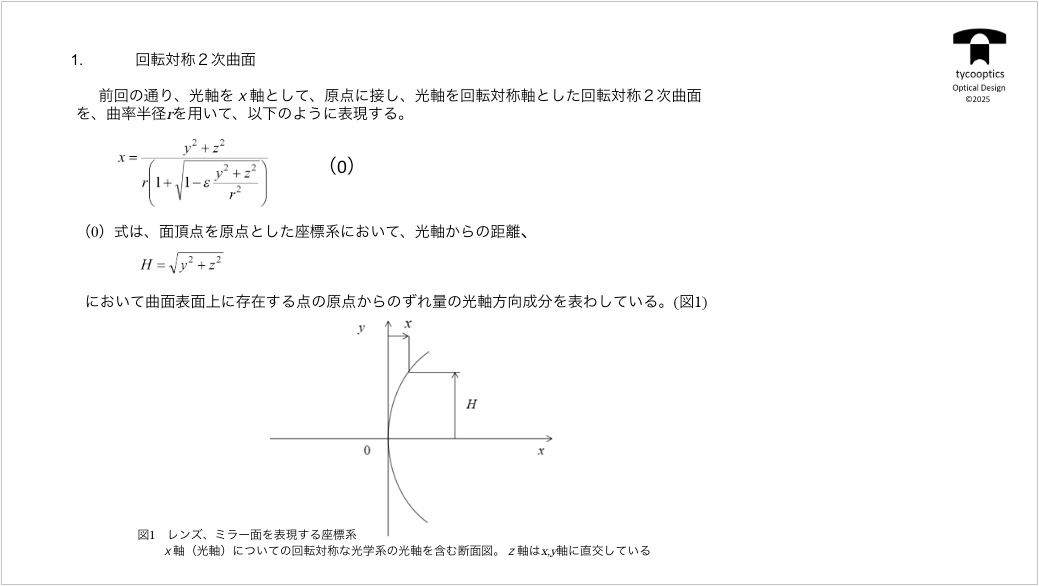
【非球面の回転対称2次曲面】
数学的な表現なんですけど、この式がございます。これが光学設計で用いる、非球面の表現式でございます。コレはもう定番ですね。
【非球面の表現形式】
こういう感じですね、1のときに球面を表します。0のときに放物と。
【付録:Zernike円形多項式の定義】
それを補うために色んな面形式が考えられていますが、とりあえずここで一つだけ。Zernikeの円形多項式というのががございます。
【FRING Zernike多項式によるfitting(回転対称成分のみ)】
コレもですね、Zernikeの多項式もさっきの回転二次の非球面形式と互換性がなくてはならないので、相互に入れ替えて使うことが本来はできるわけです。
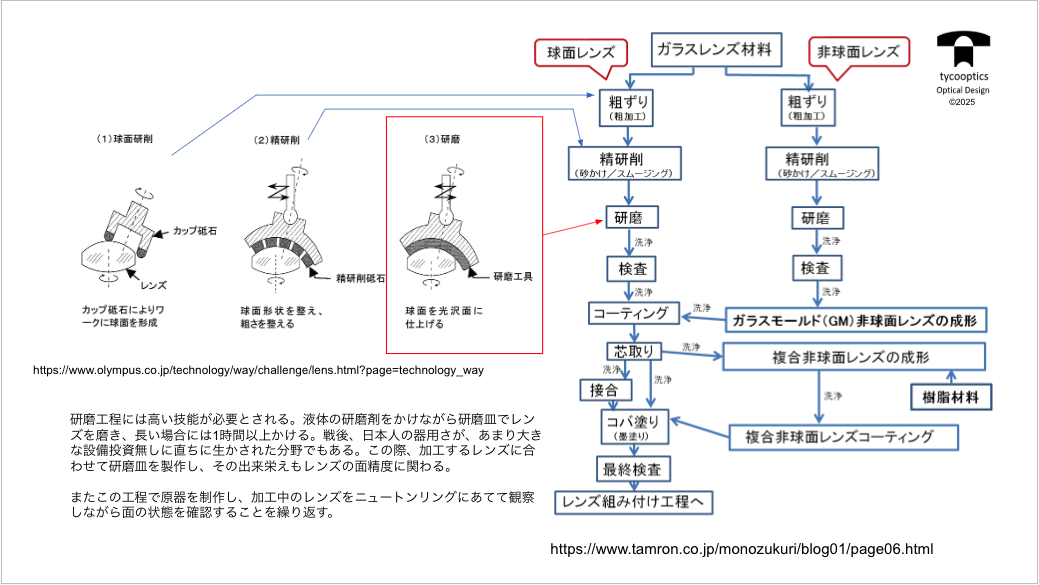
【非球面レンズ、ミラーの製造方法】
それであればですね、非球面どんどん使っていけばいいじゃないかということになるんですけども、問題は、やはり球面は回転対称性のあるものですので回転運動を使えば非常に作りやすいっていうことですね。
【収差係数と近軸計算】
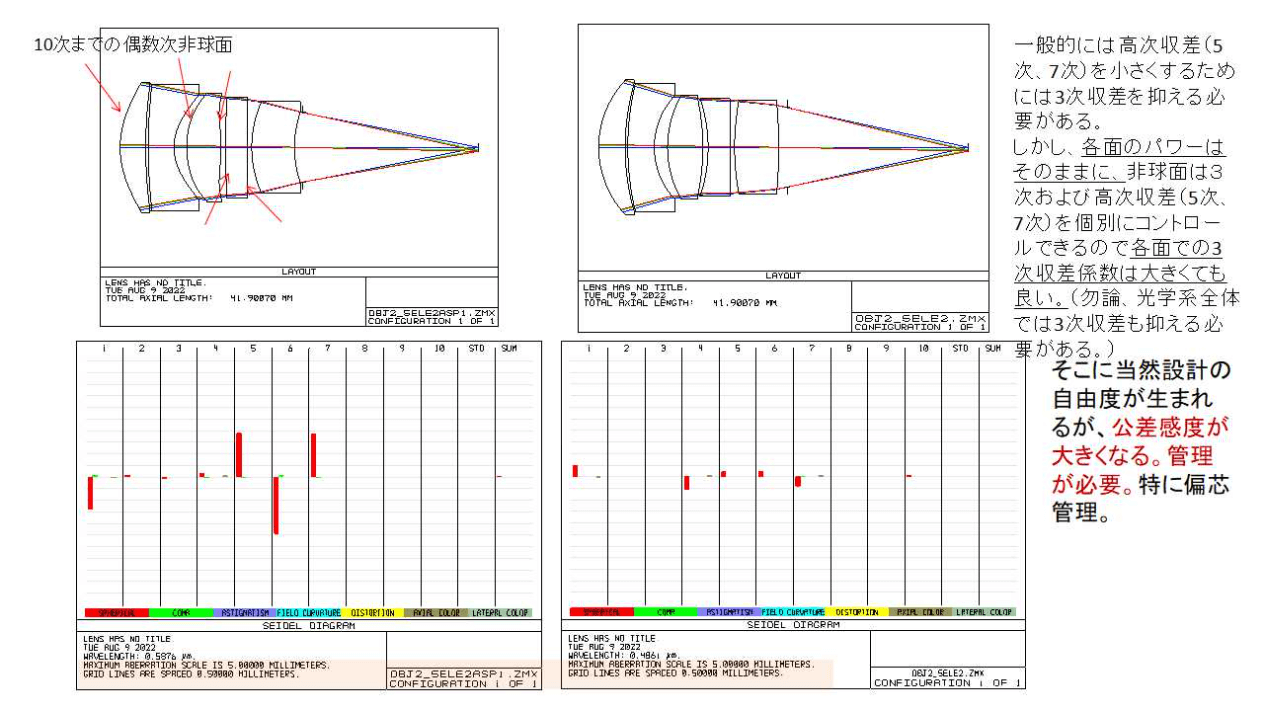
もうちょっと非球面が何故いいか、本質的な問題がございまして、例えばコレ球面収差の式、収差係数というのがありましたよね、三次収差、五次収差、七次収差というサインシータをテーラー展開していく時に、三次の項まででよしとするか、五次まで含めるか七次まで含めるかっていうことなんですけど、実際の収差っていうのはそれを全部、すごい高次のところまで合成したものが実際の収差に近くなるわけですけど、そうすると大抵の場合は、七次くらいまで合成してしまえば、相当リアルな収差の絵になるんですね。
【交差感度の大きさと管理、MTF】
デモ用に設計したものなんですけど、これゼマックスというものの画面ですね。コレ左が非球面、右は球面、実際には右で球面で設計しておいて、
非球面を導入してると、コレ結構使ってますね。
【非球面を導入する面選択の一般的指標】
どこに非球面を導入するかっていう問題なんですけど、現状では非球面をどこに用いるかっていうところまで、最適化で行けるっていうプログラムも出ていますので、コレも時間の問題でコンピューターがやってくれることになるかなと思います。
【光学系の製造について:製造公差】
やはりレンズにどのくらいの精度が必要かっていうことによってせっかく設計してもそれが実際のものに実現できないということは、どんな技術でもあることです。エンジニアリングっていうのは結局公差があるのがエンジニアリングですね。
【公差解析 Newton ringの計算】
一番の公差についてお話させていただきたいと思います。
【レーリー(Rayleigh)の理論の考え方】
例えば途中にミラーがあったりですね、ミラーで潜望鏡みたいにミラーで45度倒して上に光を分岐させてあげたりということがある場合にですね、そのミラーの精度をどのくらいまでいいのかなっていう話になるんですね。ミラーだって面精度がございますからそれによって、光は変な方向にいってしまうこともありますので、実際にはそういうことも考慮しないといけません。
【レンズ表面形状についての概観】
一体どのくらいの粗さまで追い込んでいるのかというので、第1段階の粗さでは4×10ミクロンくらいの表面の粗さなんですけど、第二段階で砂掛けで0.2ミクロンくらいまで磨きこまれるんですね。
【間隔公差 レンズ外径公差 分散公差】
間隔っていうのもありますよね。レンズができたとしてですね、面と面の間の間隔っていうのがございます。レンズを配置していくときの間隔。
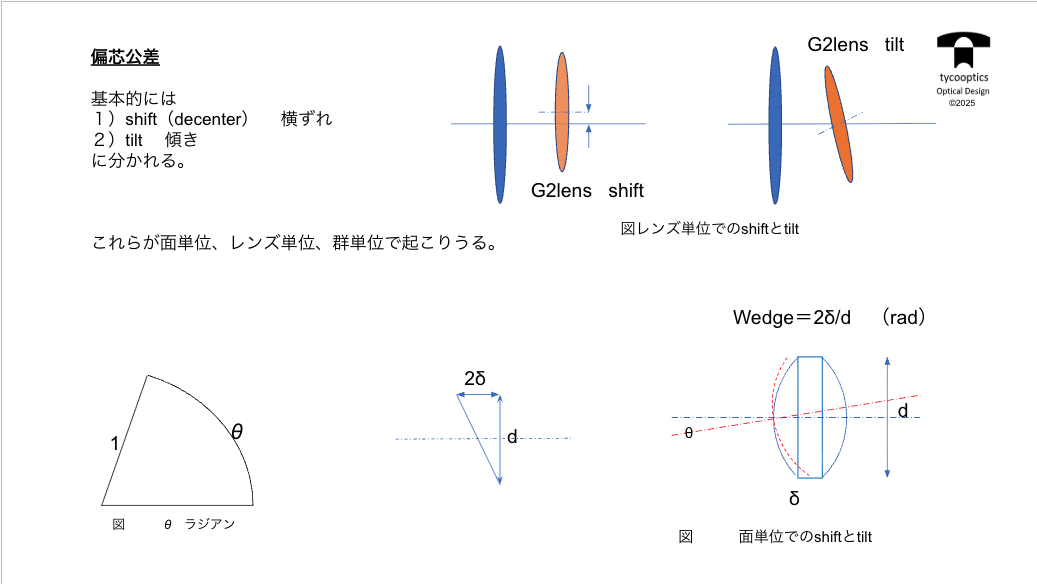
【偏芯公差】
偏芯っていうのが起きるんですね。
【芯取りとは?】
芯取りって何かなってお話ですけど、
【球面のアドバンテージ】
コレ何が便利かっていうと、
【調芯の例】
今実際にレンズメーカーさんで行われていることなんですけど、
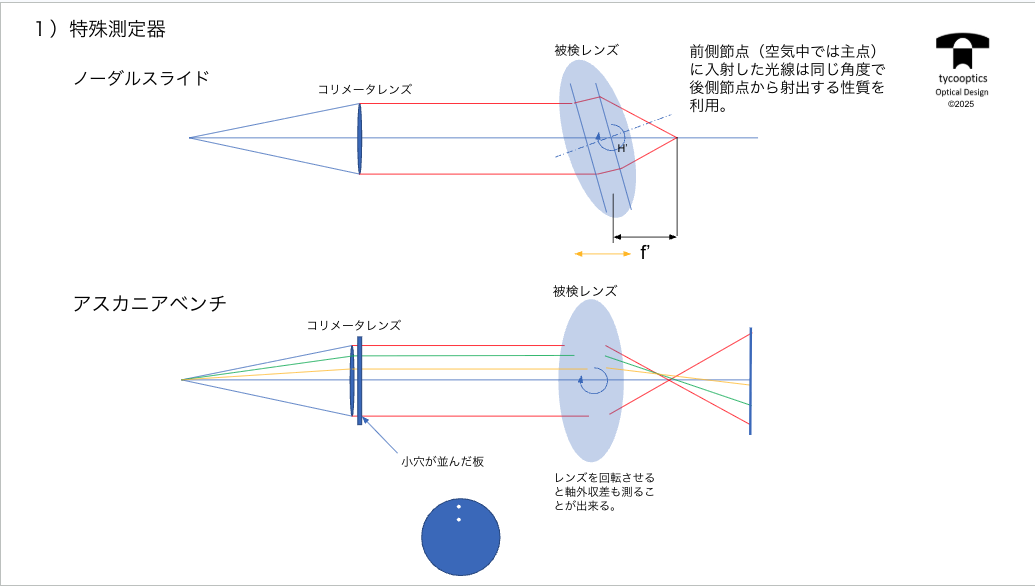
【特殊測定器】
じゃあレンズってどうやってできたもの測定するのかっていうことでまとめました。
【撮影測定とMTF測定】
撮影したり目視したりして、チャートを解像してるということですね。
【低周波数MTF、そしてPTFの影響】
MTFをどうやって測定しているのかという話になります。
【波面収差による管理】
ニュートンリングでわからないんだったら波面を見なくてはいけない。
【一般公差の最後に】
【温度特性評価】
温度特性と、ゴーストフレアについてご説明させていただきます。
【屈折率の温度変化】
これはですね、温度特性屈折率が温度によって変化してしまうという重要な事実です。
【材質により異なる温度依存特性】
屈折率が変わると同時にガラスが膨張しますよね、温度が上がると。
【レンズ・バルサムの使用条件ガイドライン】
プラスチック系は温度で変わってしまうのでそのまま使うとたしかに厳しい。
【プラスティックレンズを使用する際のコツ】
プラレンズをやっぱり使いたい場合ですね、どういう使い方のコツがあるかというとですね
【色収差と温度特性収差の関係】
色収差っていうのは、波長が変わることによって、屈折率が変わる
【ゴースト・フレア評価 / 改善】
ここらへんの温度特性は非常にシビアなんで、なかなかプラレンズには使いにくいっていうところはあります。
【一括のゴーストシミュレーション】
これは、内面反射のことです。
【フレネル反射によるゴースト】
【フレネル反射と全反射によるゴースト】
【撮像素子による反射】
【これからの光学設計】
【質疑応答】
レーザー・光学の動画学習サービス OptiVideo
豊富なレーザー・光学の動画コンテンツが定額で見放題で、他では聞けない有名な先生の講義が視聴可能です。
労働安全衛生法やJIS C6802を網羅したレーザー安全の講義内容を発信。
使用者、管理者にマストな、あらゆる危険に備える知識を「OptiVideo」で学べます。
また、月1回以上のWebセミナー講習が無料で聴講可能です。