目次
セミナーを内容を紹介しています。
⊕タイトル部分をクリックしていただくと詳細をご覧いただけます。
-
光学の歴史と幾何光学(1)(1:55:45)
-
- 人は光をどう理解してきたか?
- イスラムの光学(AC9世紀)
- ルネッサンス以降
- 近代へ
-
- ANTONY VAN LEEUWENHORK(1632-1723)
- 単レンズ式顕微鏡ROBERT HOOKE(1653-1703)
- ISAAC NEWTON(1642-1727)
- 光の時代へ
- 光の波長
-
- 太陽の光
- 光学・光学入門
- 光線
-
- 反射と屈折
- 屈折
- 反射
- 屈折率
- 屈折率(分散)
- 屈折率と光速
-
- ニュートンの実験(太陽光の分散)
- フェルマーの原理
- 屈折
-
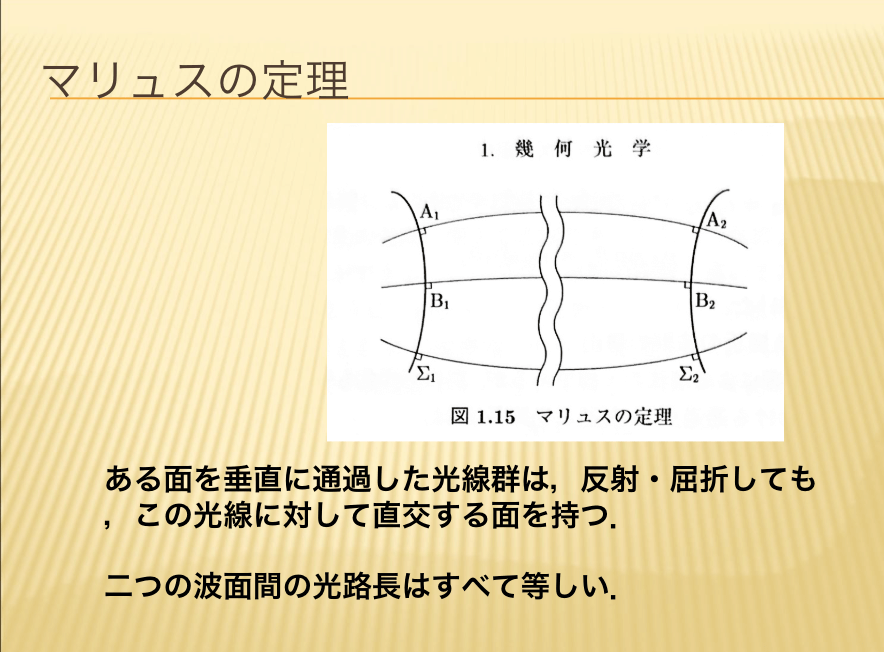
- マリュスの定理
- 全反射
-
- 光学系における距離の取り方,符号
- 近軸光線 (球面における屈折(1)
-
- 球面における屈折(2)
- ラグランジュの不変量
- 焦点距離
- ニュートンの式
-
- 倍率(横倍率)
- 倍率(縦倍率,角倍率)
- 球面における反射
- 薄肉レンズ(1)
- 薄肉レンズ(2)
-
- レンズのパワー(屈折力)
- 薄肉レンズの組み合わせ
- 厚肉レンズ
-
- 質疑応答
-
-
幾何光学(2)(2:03:31)
-
- 光学系における距離の取り方、符号
- 近軸光線{球面における屈折(1)}
- 球面における屈折(2)
-
- ラグランジュの不変量
- 焦点距離
- ニュートンの式
- 倍率(横倍率)
- 倍率(縦倍率,角倍率)
- 球面における反射
- 薄肉レンズ(1)
-
- 薄肉レンズ(2)
- レンズのパワー(屈折力)
- 薄肉レンズの組み合わせ
-
- 厚肉レンズ
- 主要点(主点,節点)
- 二つの光学系の結合
- アフォーカル光学系
-
- ベンディング
- 絞り
-
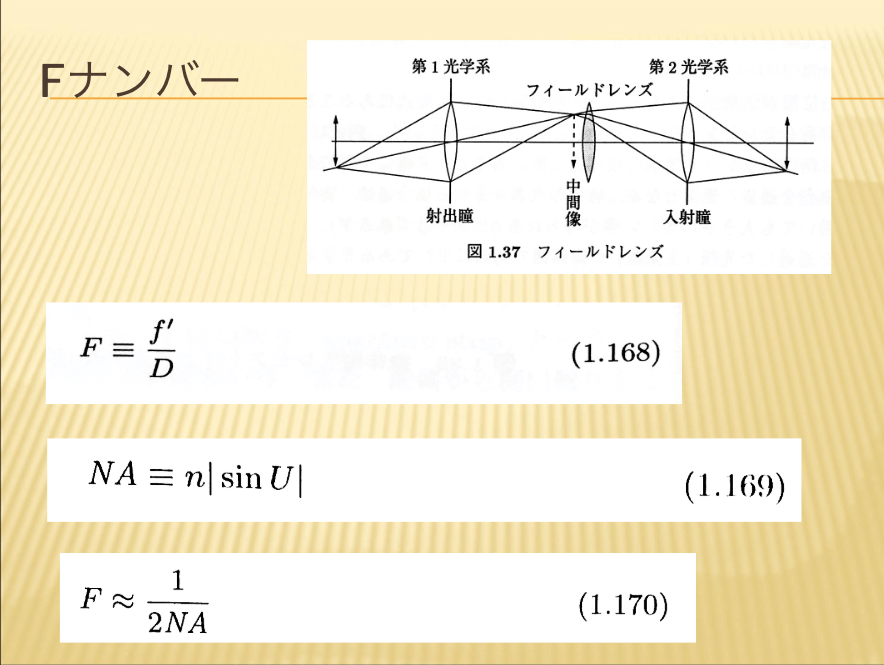
- Fナンバー
- 収差
-
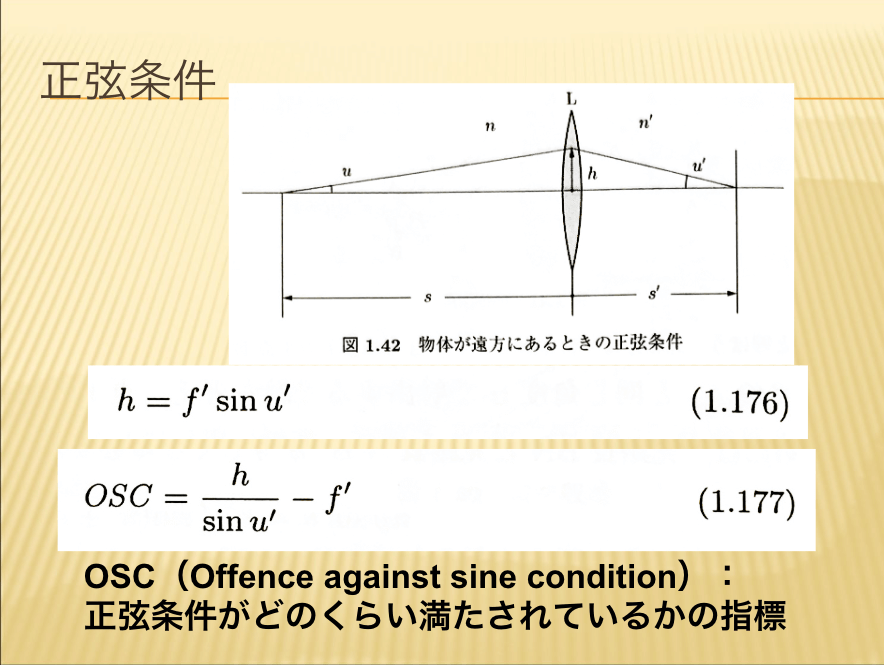
- 正弦条件
- アプラナティック球面レンズ
-
- 非点収差
- 像面湾曲
- 歪曲
- 色収差
- アッべ数
-
- 色消しレンズ
- 球面収差
- 拡大鏡(ルーペ)
- 顕微鏡
-
- 望遠鏡
- 近軸光線の追跡(行列表示)
- 光線ベクトル
- 光学系行列
- 厚肉レンズ
-
-
波動としての光(1:52:21)
-
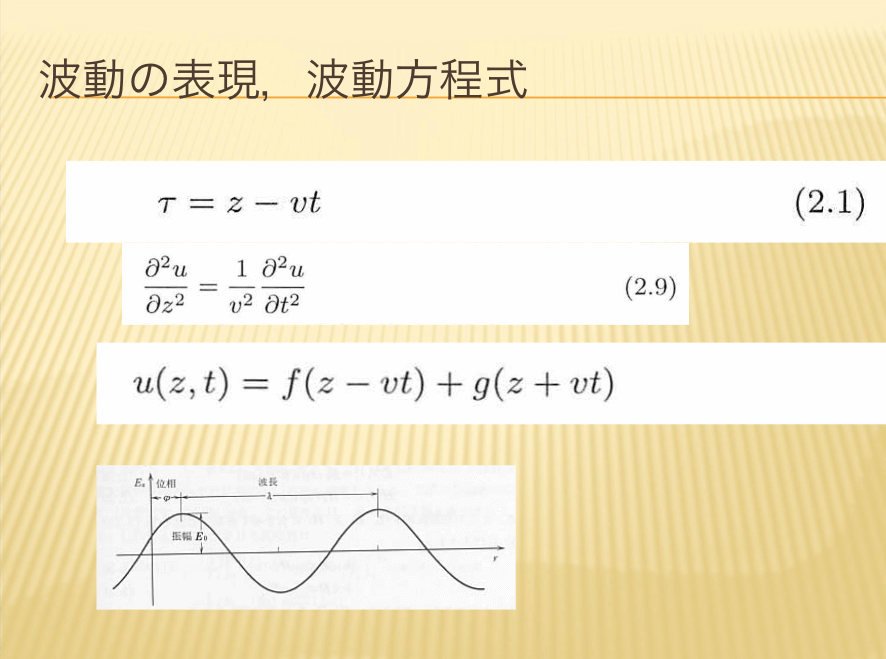
- 波動の条件、波動方程式
- 波動方程式
- マックスウェルの方程式
-
- 波動方程式
- 正弦波
-
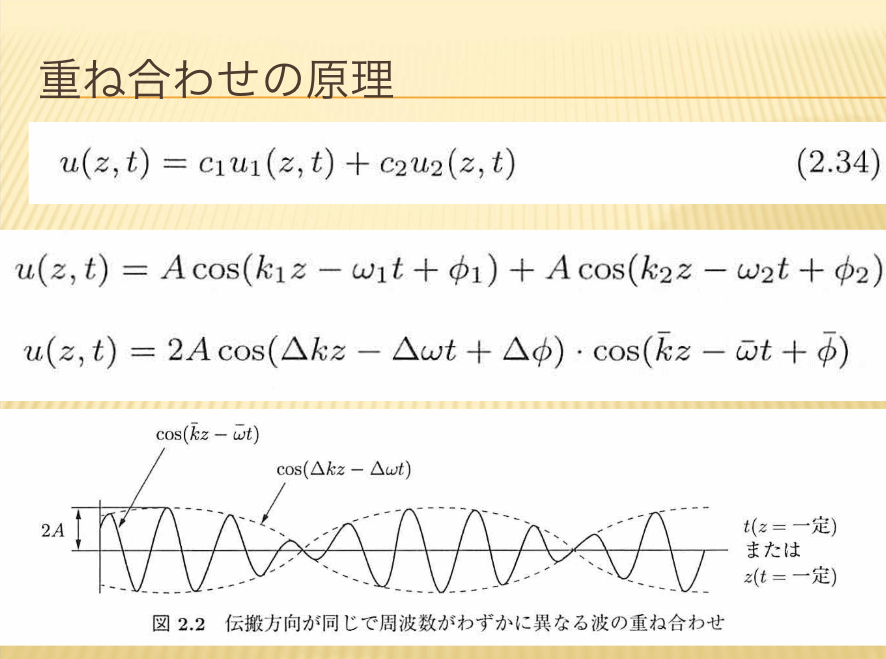
- 重ね合わせの原理
- 位相速度と群速度
-
- 波動の複数表示
- 平面波
- 球面波
-
- 重ね合わせの原理とフーリエ変換
- 波のエネルギー
- 電磁波のエネルギの流れ:ポインティングベクトル
- 横波としての電磁波
-
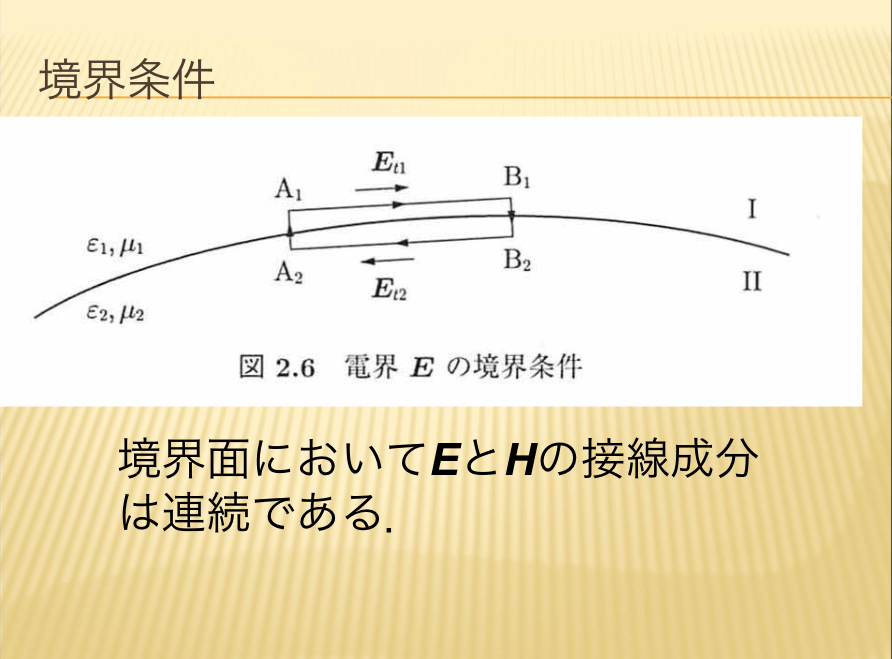
- 境界条件
- 波の反射と屈折
- 波の反射と屈折(スネルの法則)
-
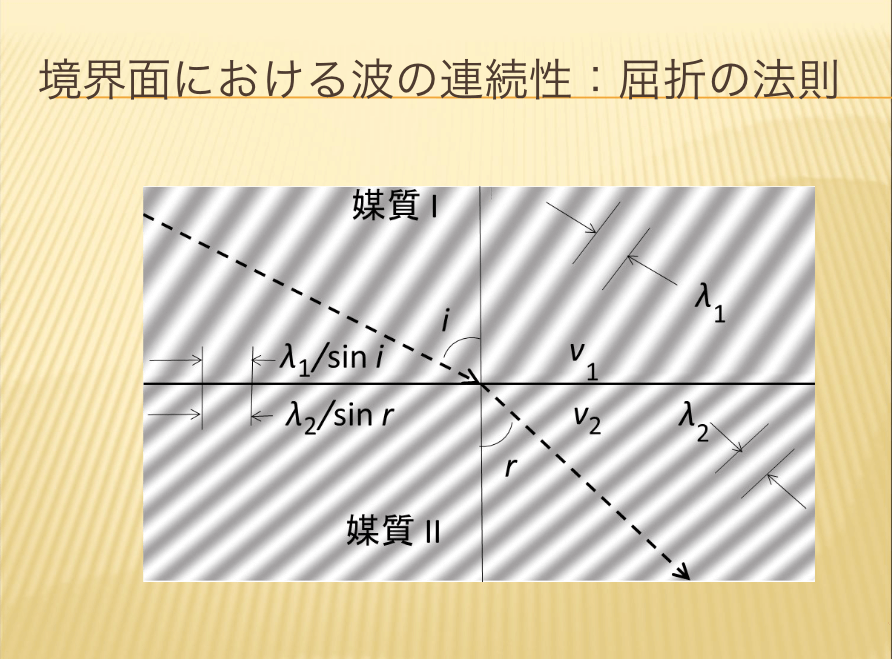
- 境界面における波の連続性:屈折の法則
- フレネルの反射透過係数
- ベクトルの公式
-
- S-偏光の場合
- P-偏光の場合
- 振幅透過率・反射率(フレネル係数)
- ブリュースター角
-
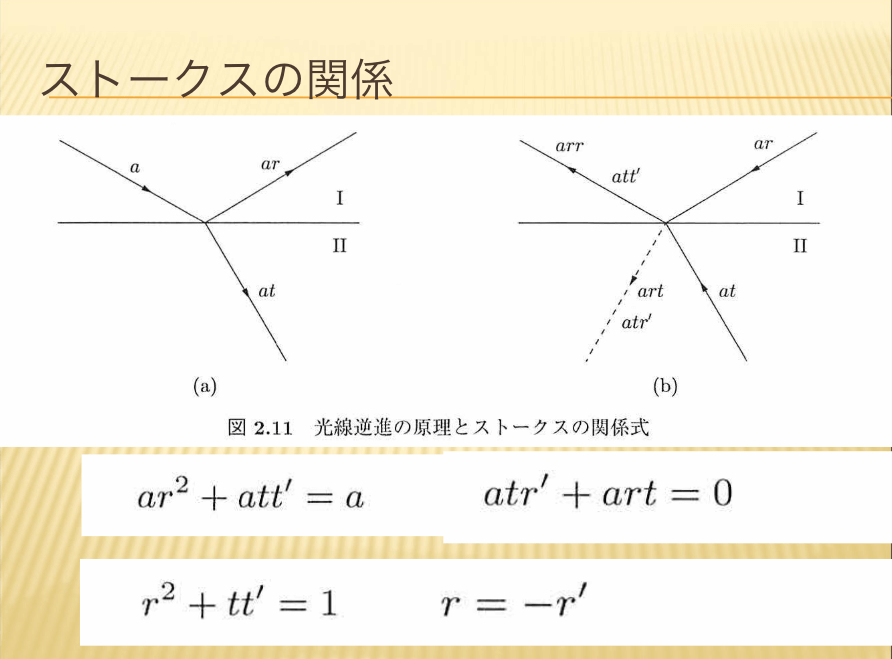
- ストークスの関係
- 強度反射率と強度透過率
-
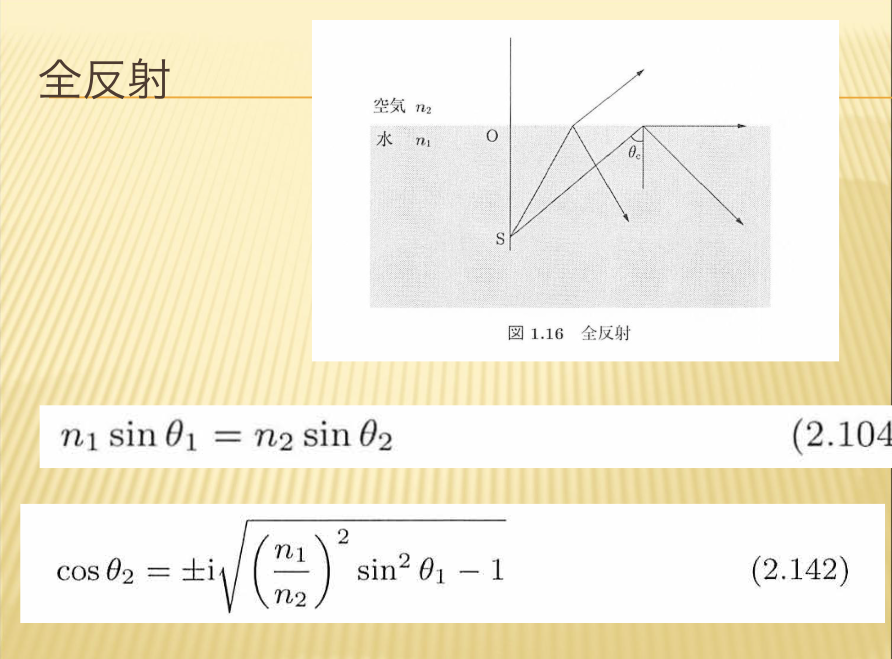
- 全反射
-
-
偏光(1:43:33)
-
- 偏光の表し方
-
- 直線偏光
- 円偏光
-
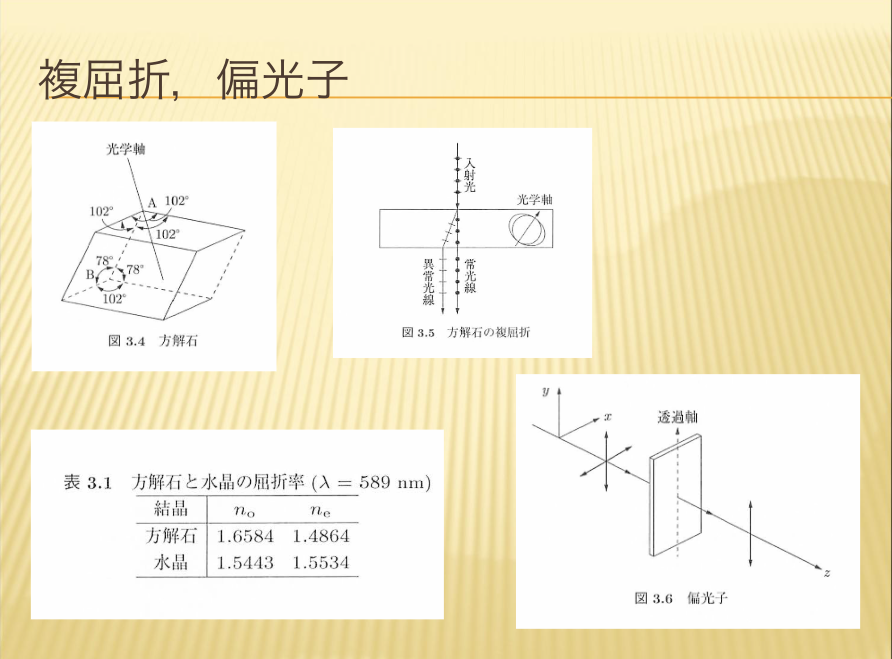
- 複屈折,偏光子
- 波長板
-
- ストークスパラメーター
- スタークスパラメーターの測定
- 部分偏光
-
- ミューラー行列
- 偏光子
- 波長板
- 旋光子
-
- 角度θ回転させたミューラー行列
- X軸に対して45°の直線偏光が1/4波長板を通過した場合
-
- ポアンカレ球
- ジョーンズベクトル
- ジョーンズ行列
-
- 波長板の回転
- 直交直線偏光子
- アイソレーター
-
- 質疑応答
-
-
干渉(2:02:53)
-
- ヤングの実験
-
- 白色光干渉
- 干渉縞の鮮明度
- 時間的可干渉性
-
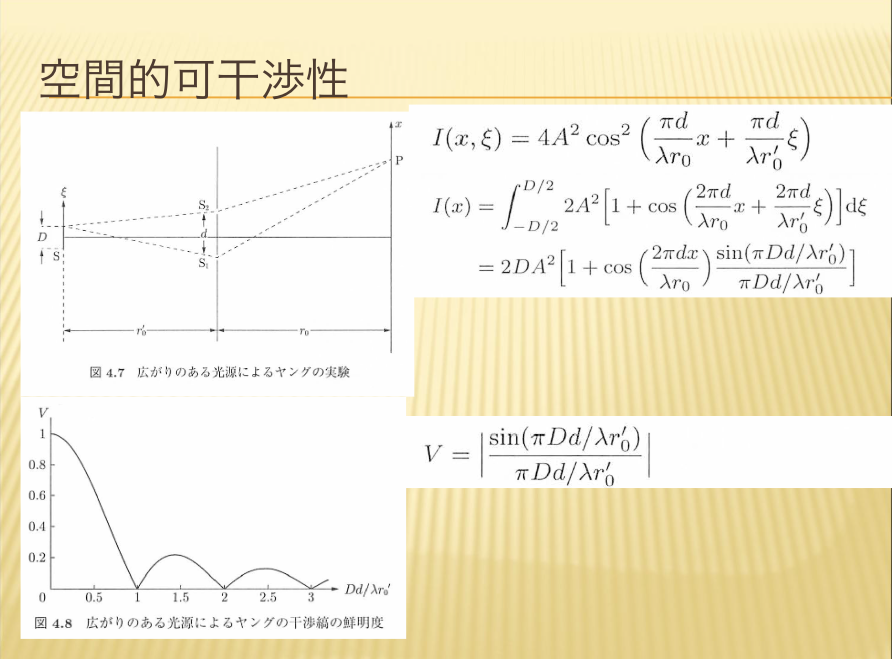
- 空間的可干渉性
- ファンシッター・ツエルニケの定理
-
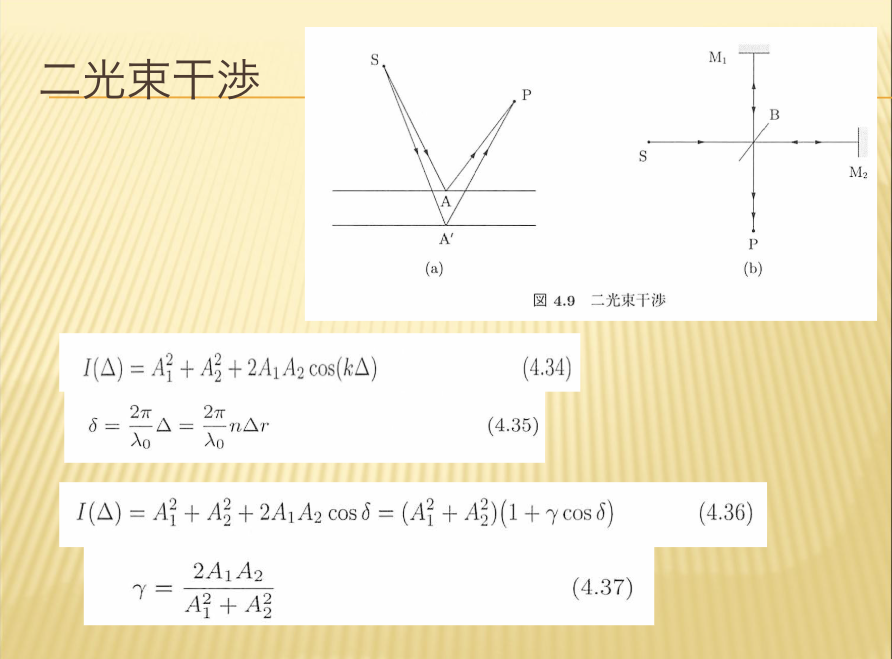
- 二光束干渉
- 等傾角干渉
-
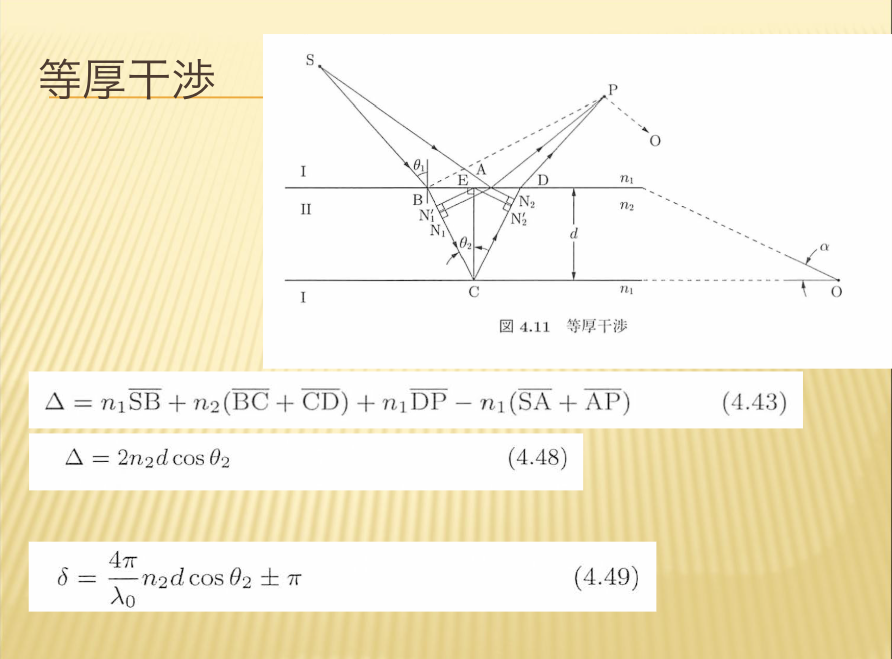
- 等厚干渉
- ニュートンリング
-
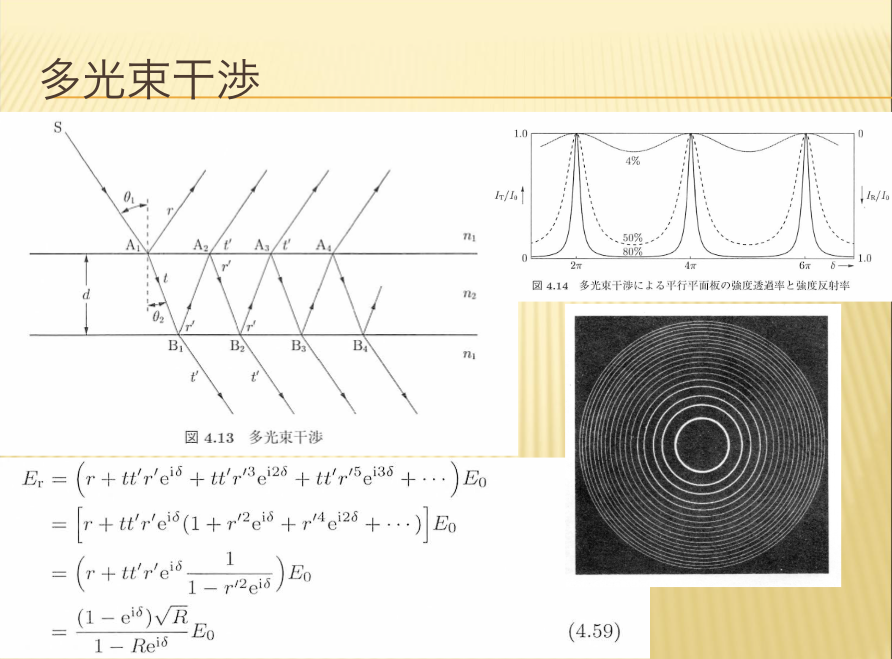
- 多光束干渉
-
- 反射防止膜
- 多層膜における干渉
-
- 特性行列
- 反射率と透過率
- 多層反射膜
-
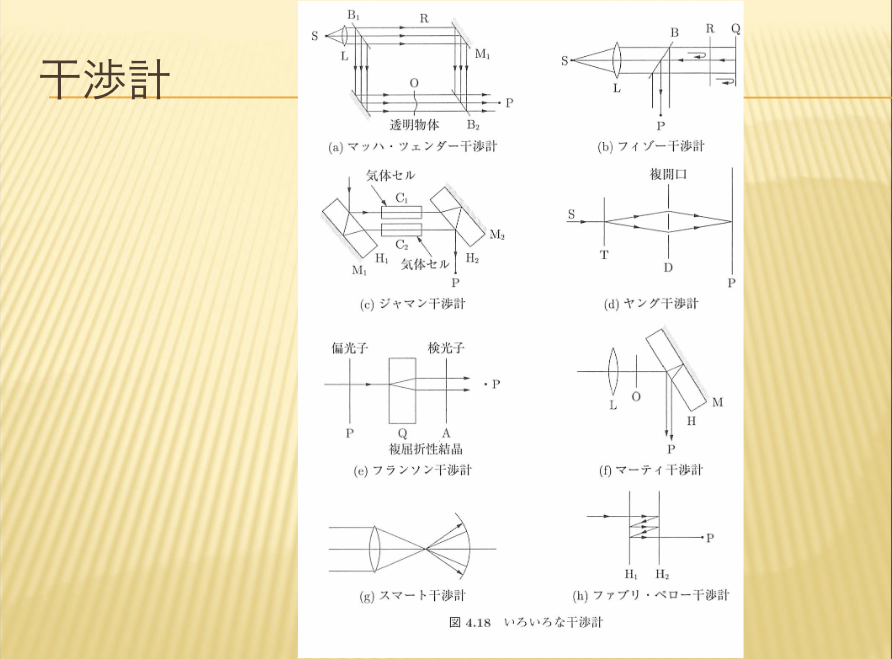
- 干渉計
- マイケルソン干渉計
- トワイマン・グリーン干渉計
-
- フィゾー干渉計
-
-
回析(1:45:28)
-
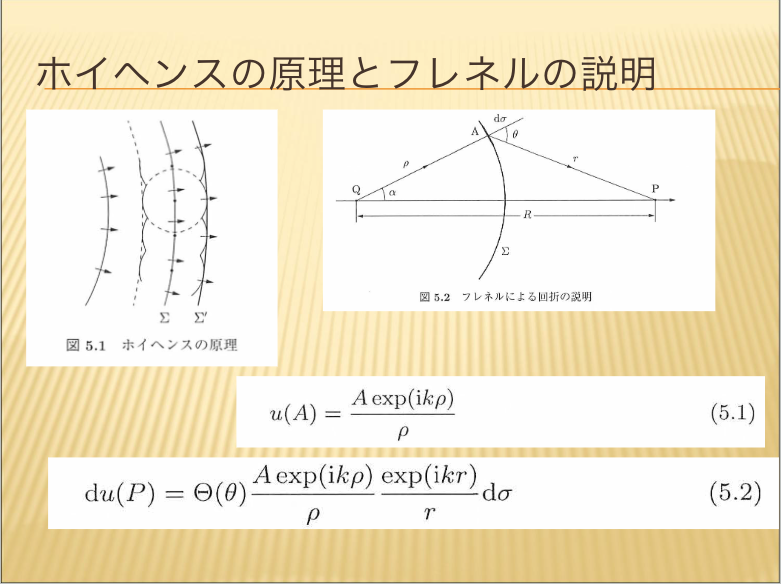
- ホイヘンスの原理とフレネルの説明
-
- フレネル・キルヒホッフの回折式
-
- バネビの定理
- フレネル回折
-
- フラウンホーファー回折
- スリットのフラウンホーファー回折
-
- 矩形開口のフラウンホーファー回折
- 横ずれしたスリットのフラウンホーファー回折
- 複スリットのフラウンホーファー回折
-
- 回折格子
- 円形開口のフラウンホーファー回折
-
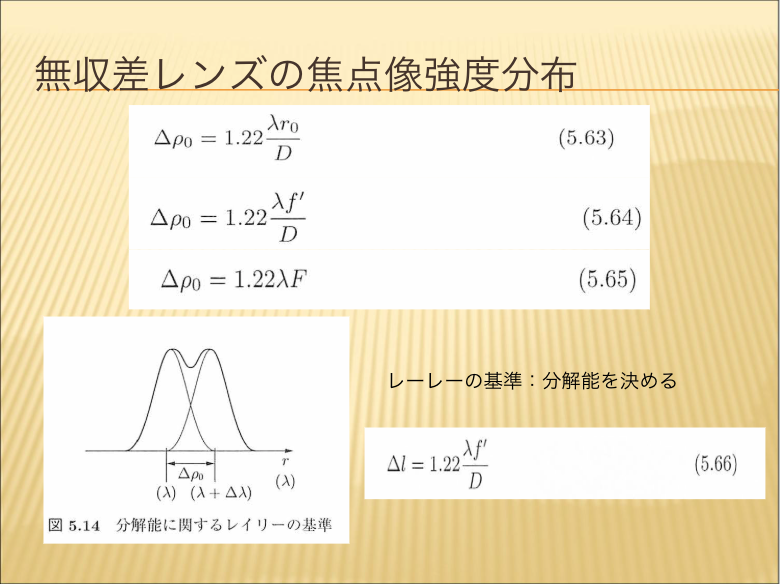
- 無収差レンズの焦点像強度分布
- フレネル回折
-
- コルニューの螺旋
- ナイフエッジのフレネル回折
- スリットのフレネル回折
- 円形開口のフレネル回折
- フレネルゾーンプレート
-
- 角スペクトル法
-
- 質疑応答
-
-
フーリエ光学(1:54:14)
-
- フーリエ光学の教科書
- フーリエ変換とコンボリューション
-
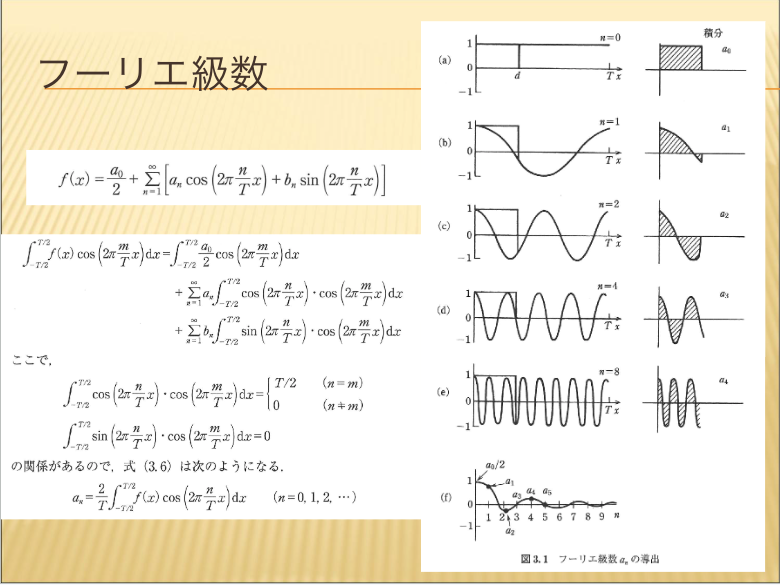
- フーリエ級数
- 2次元
- コンボリューション積分
-
- フーリエ変換の性質
- よく使う関数とフーリエ変換
- フレネル回折とコンボリューション積分
-
- フレネル回折式(別の変形)
- 角スペクトル法
-
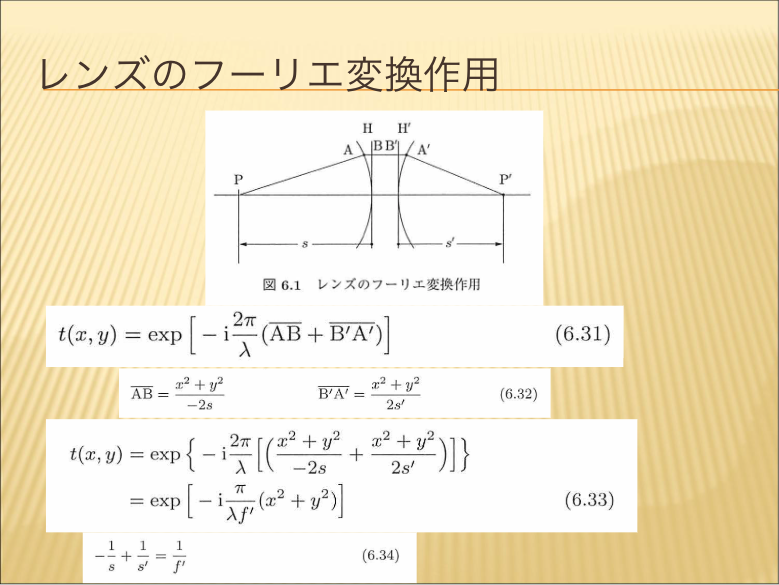
- レンズのフーリエ変換作用
-
- 結像
- コーヒーレント光学系の伝達関数
-
- インコヒーレント結像の伝達関数
- インコヒーレント結像のOTF
-
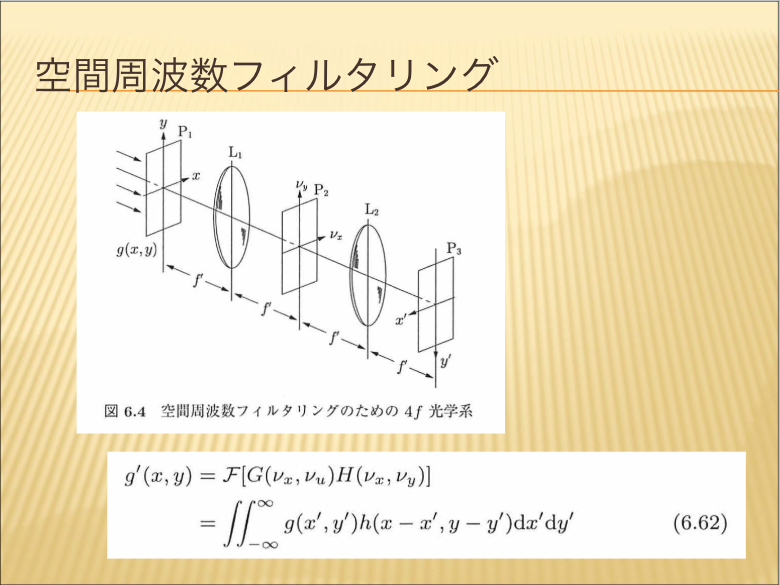
- 空間周波数フィルタリング
- 周波数制限フィルター
- マッチトフィルター
- 結合フーリエ変換相関器
- ホログラフィ
- ホログラムの種類
-
- 計算機ホログラム
- ディジタルホログラフィ
- ホログラフィの応用
- ホログラフィ干渉
-
- 質疑応答
-
-
物質と光(1:51:15)
-
- 電子双極子モーメント
-
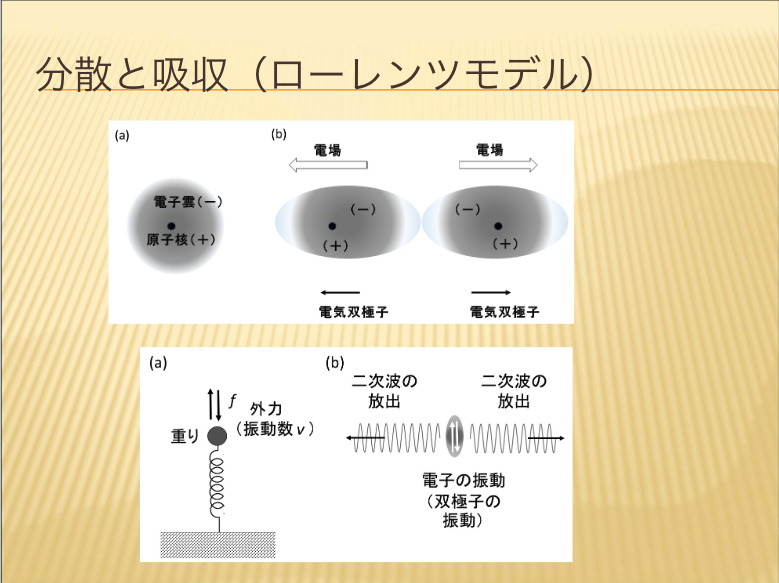
- 分散と吸収(ローレンツモデル)
- ローレンツモデル(気体の場合)part1
-
- ローレンツモデル(気体の場合)part2
-
- ローレンツモデル(液体・固体の場合)
-
- ローレンツモデル( 液体・固体の場合)
- 金属の屈折率分散
- 自由電子だけの効果
-
- 発光と受光
- 双極子からの放射
- 電気双極子の振動はZ方向とする
- 双極子から十分離れたところでは
- 双極子による電磁波の放射
- 黒体からの光放射(プランクの式)
-
- 自然放出と誘導放出
- 蛍光とLED
- レーザー
- 半導体励起固体レーザー(DPSS)
- ファイバーレーザー
-
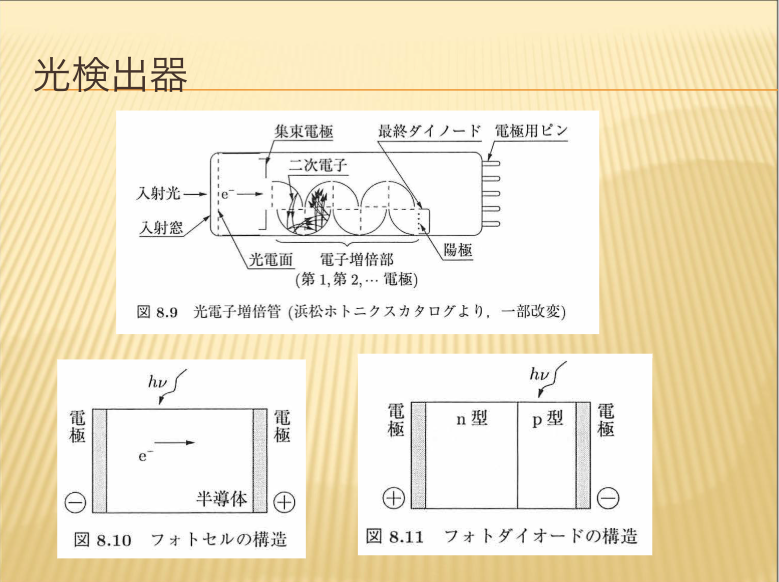
- 光検出器
- 固体撮像素子
-
- 散乱と吸収
- ランバート・ベールの法則
- 「逆方向にすすむ光束が無視できる場合」「ランバートの法則」
- 「散乱が無視できて、吸収がその濃度に比例する時」ベールの法則
- クベルカ・ムンクの式
- 微粒子や媒質による散乱
- 散乱断面積
- 散乱式
-
- レイリー散乱
-
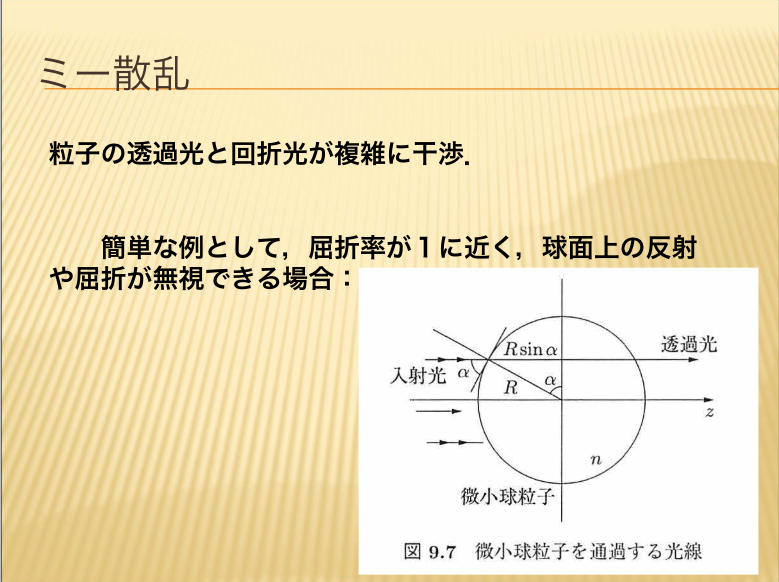
- ミー散乱
- 火星の夕日は青い!
- 表面による反射
-
-
非等方媒質中の光(1:45:07)
-
- 誘電率テンソル
-
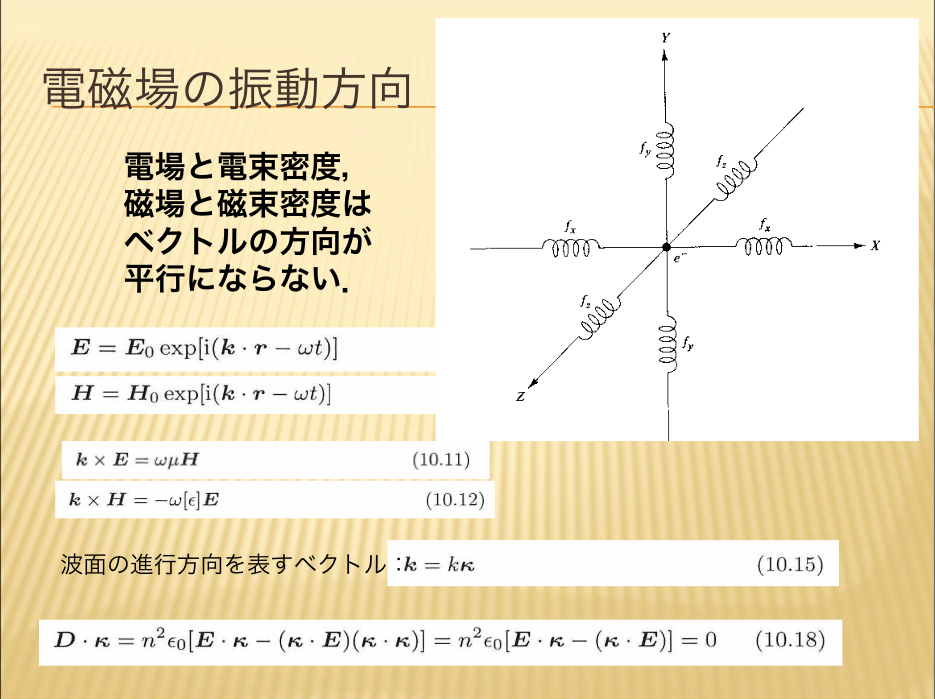
- 電磁場の振動方向
-
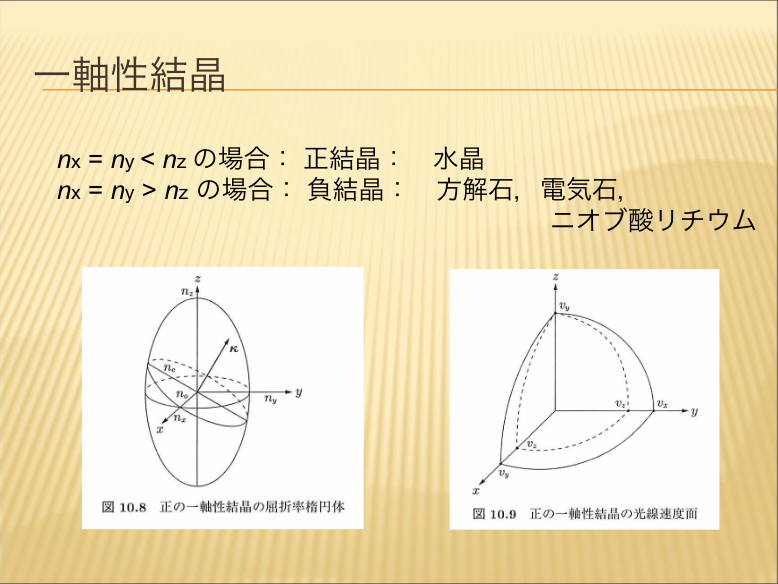
- 屈折率楕円体
-
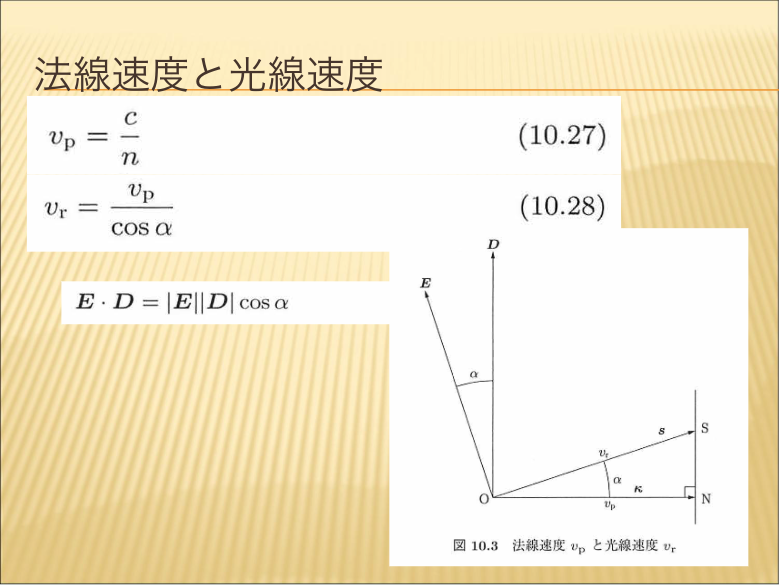
- 法線速度と光線速度
- 法線速度面
-
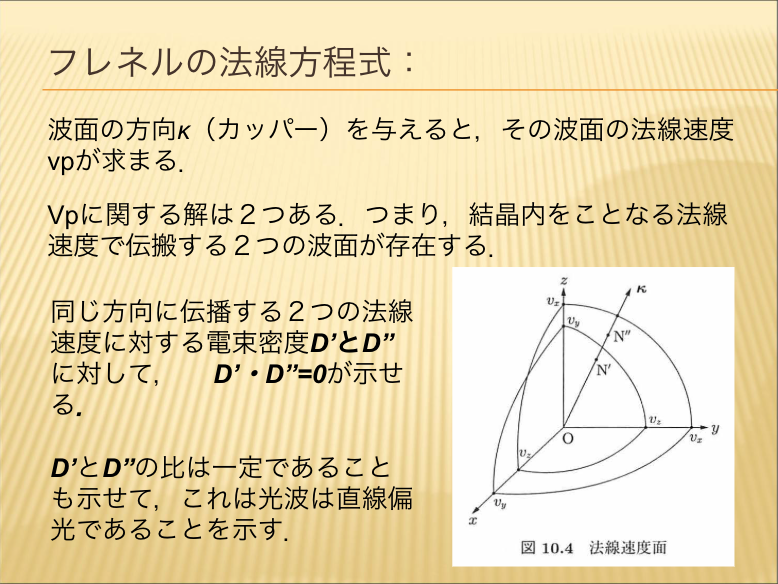
- フレネルの法線方程式
- 屈折率面
-
- 光線速度
- 光線速度面
-
- 一軸性結晶
- 常光線と異常光線
- 異常光線の屈折
-
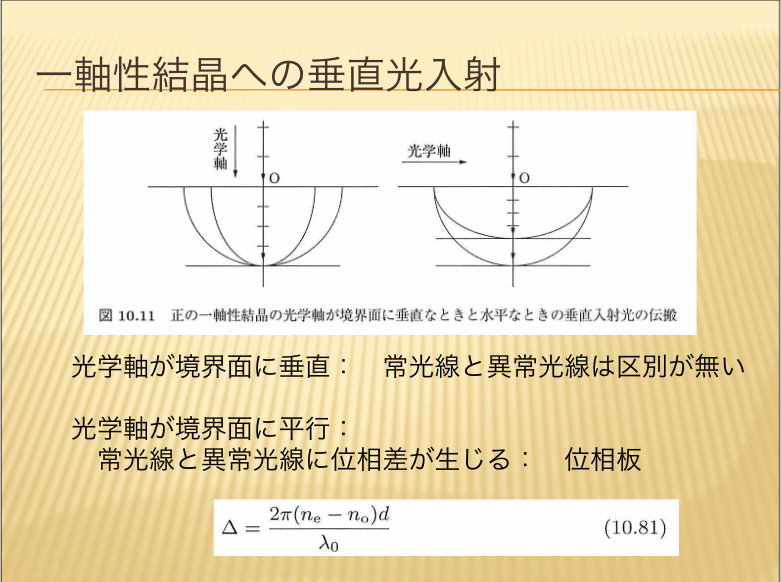
- 一軸性結晶への垂直光入射
- 一軸性結晶への斜め入射
-
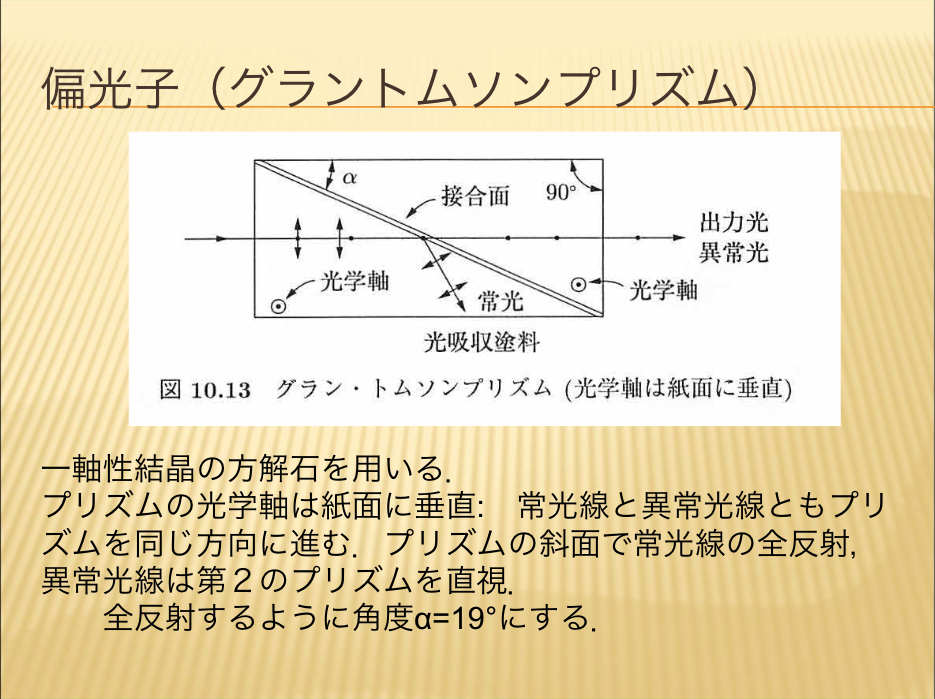
- 偏光子(グラントムソンプリズム)
- 黒体からの光放射(プランクの式)
- 位相板
- 複像プリズム
- 光学活性(OPTICAL ACTIVITY)
- 二色性(DICHROISM)
- 液晶
-
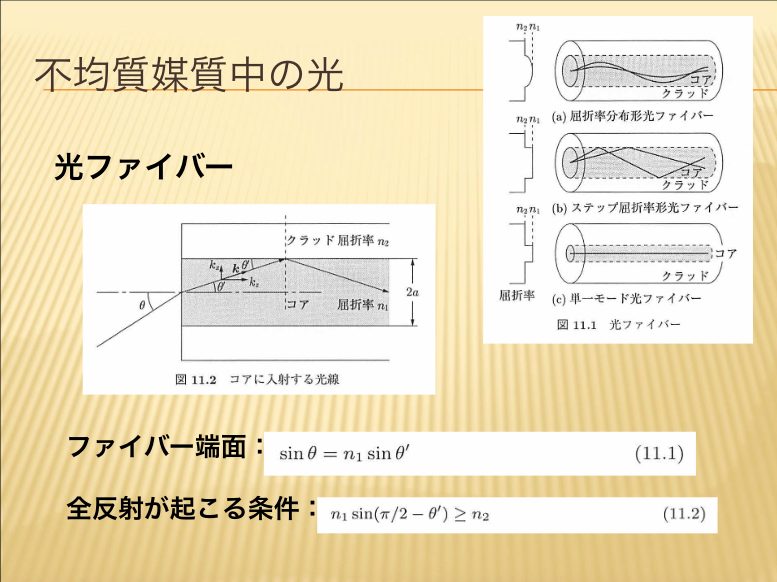
- 光ファイバー
- アイコナール(EIKONAL)
-
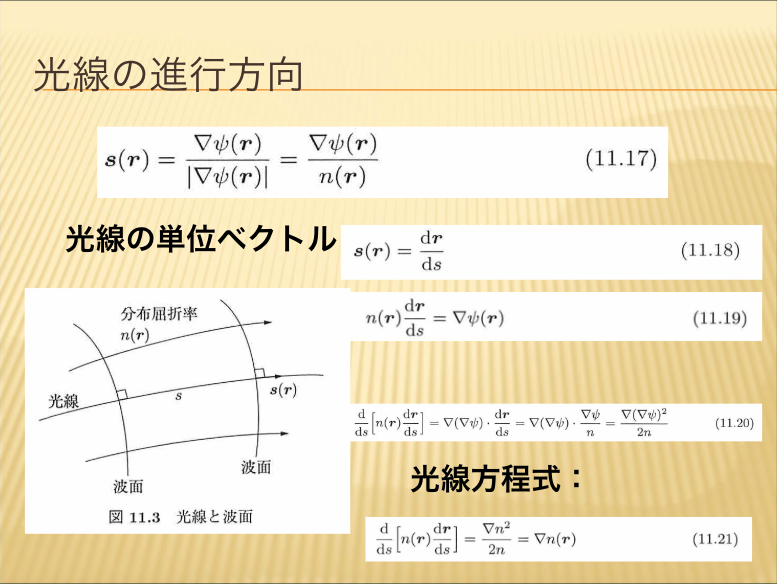
- 光線の進行方向
- 屈折率分布型光導波路
-
-
測光と測色 ガウスビームの伝播(1:40:50)
-
- ガウスビームの伝搬
- 近軸ヘルムホルツ方程式の解
-
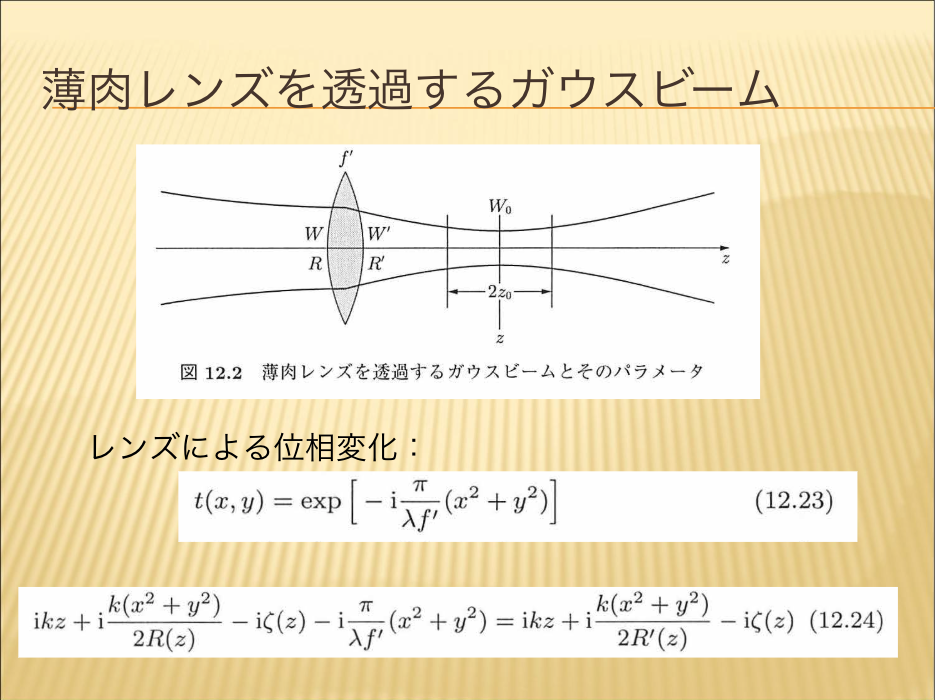
- 薄肉レンズを通過するガウスビーム
- 行列によるガウスビームの伝搬
-
- 測光
- 立体角
- 放射量と測光量
-
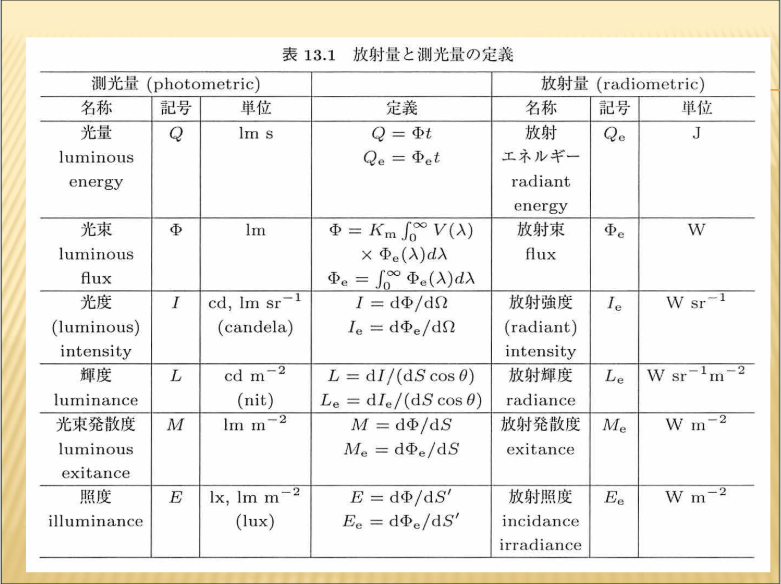
- 放射量と測光量の定義
- 光度、輝度、光束発散度
-
- 照度
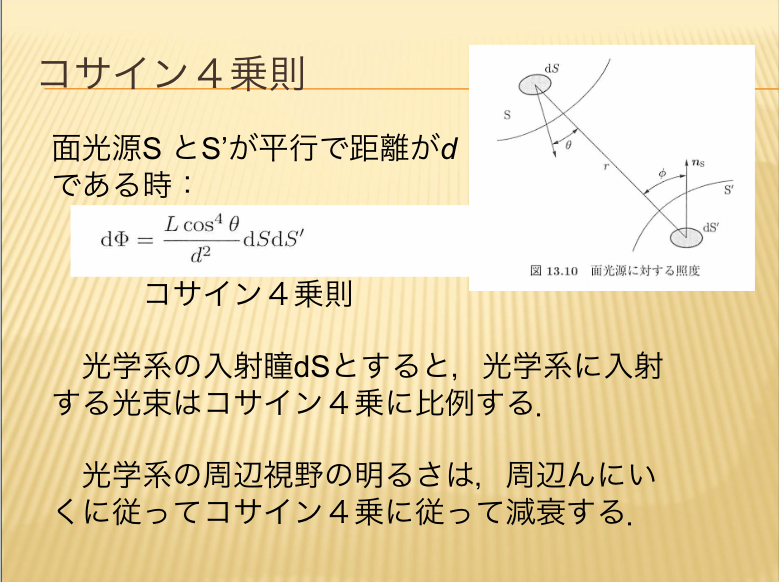
- 面光源の場合
- 完全拡散光源
-
- コサイン4乗則
- 測色
- 加法混色
-
- RGB表示色
- XYZ表示色
-
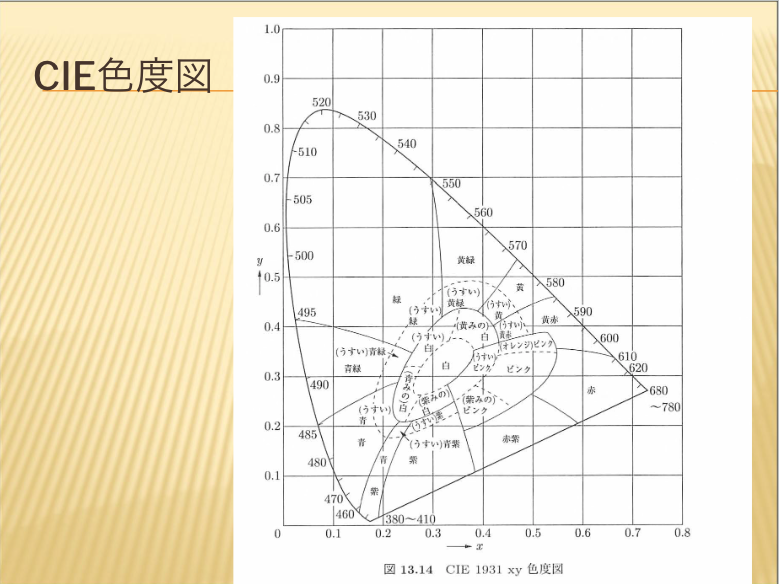
- CIE色度図
- 白色・色温度
-
- 質疑応答
-
光学の歴史と幾何光学(1)
【人は光をどう理解してきたか?】
光はとにかく目で見えるためたいへん分かりやすい現象ですが、あまりにも身近すぎて、「光とは何か」と考えた人は、昔は恐らく少なかったのではないかと思われます。当たり前に存在するものだと思われていた光を、どのように学問づけ、現代に至ったかということをお話しします。
【イスラムの光学(AC9世紀)】
1000年以上に渡り、ヨーロッパは暗黒時代と言われていましたが、その間には、実はイスラムでは科学が非常に発達しました。イラク出身のアルハーゼンの著書「光学」では、光の屈折や球面の反射、レンズの原理や目の構造などが記されています。今我々が理解してる認識が、既に9世紀頃のイスラムではほぼ存在していたのです。
【ルネッサンス以降】
ルネッサンス以降では、ガリレオが望遠鏡を作成しました。その後ケプラーが別の原理を用いて、ケプラー式といわれる望遠鏡を考えました。それからフェルマーの原理が見つかり、光は空間をどのように伝わるのかという基本的な原理が述べられました。
【近代へ】
近代になると、レーヴェンフックが単レンズの顕微鏡で赤血球や微生物、精子を初めて発見しました。フックは、顕微鏡で見た資料の絵をミクログラフィアという著書にまとめ、大ベストセラーになりました。それから1800年頃、ヤングが干渉の現象を用いて、光は波動だということを証明しました。
【ANTONY VAN LEEUWENHORK(1632-1723)】
顕微鏡を作った人物です。
【単レンズ式顕微鏡】
ANTONY VAN LEEUWENHORKはが作成した顕微鏡のレンズの直径は約1ミリ程で、倍率が200倍400倍近くあったといわれています。視野が非常に狭いと、中心付近は非常に鮮明に見えますが、少し中心が外れるとすぐぼやけてしまう欠点がありました。
【ROBERT HOOKE(1653-1703)】
ロバートフックの肖像画ですが、最近では間違いということになっています。ロバートフックの肖像画は残っておらず、ニュートンと仲が悪く、フックの死後、ニュートンが全部処分したといわれています。彼の著書「ミクログラフィア」では、自身で作成した望遠鏡で実際に見た月の表面などが描かれています。
【ISAAC NEWTON(1642-1727)】
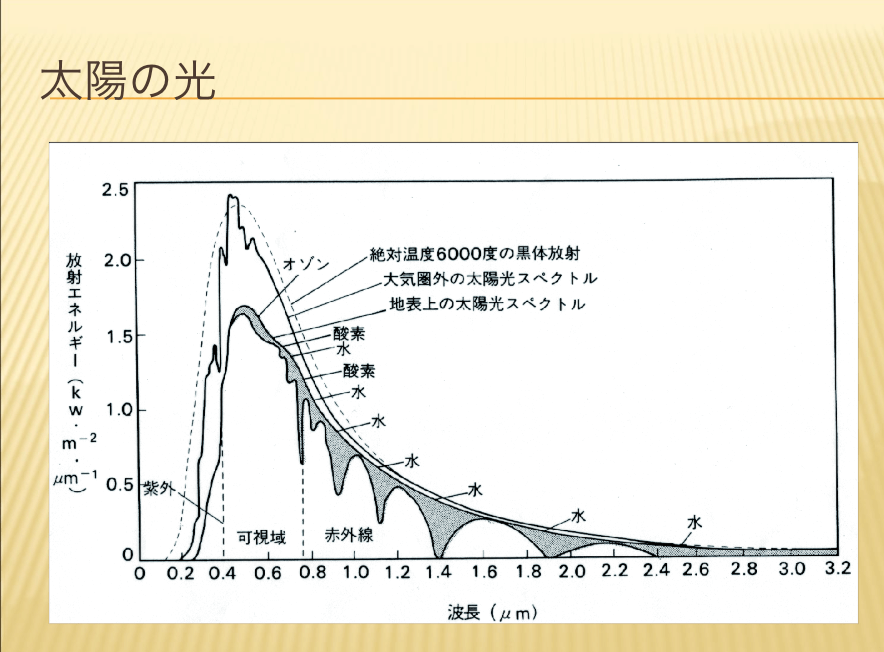
ニュートンは光の粒子説を唱え、太陽光のスペクトルを分解と合成を行い、反射望遠鏡を作成した人物です。
【光の時代へ】
20世紀に入り量子が生まれると、それをもとに冷蔵庫の発明されるなど、光技術は我々の生活に身近なものになりました。現在では非常に短いパルスの作成が可能になるなど、いよいよ現実のものとして使われつつある時代になってきました。
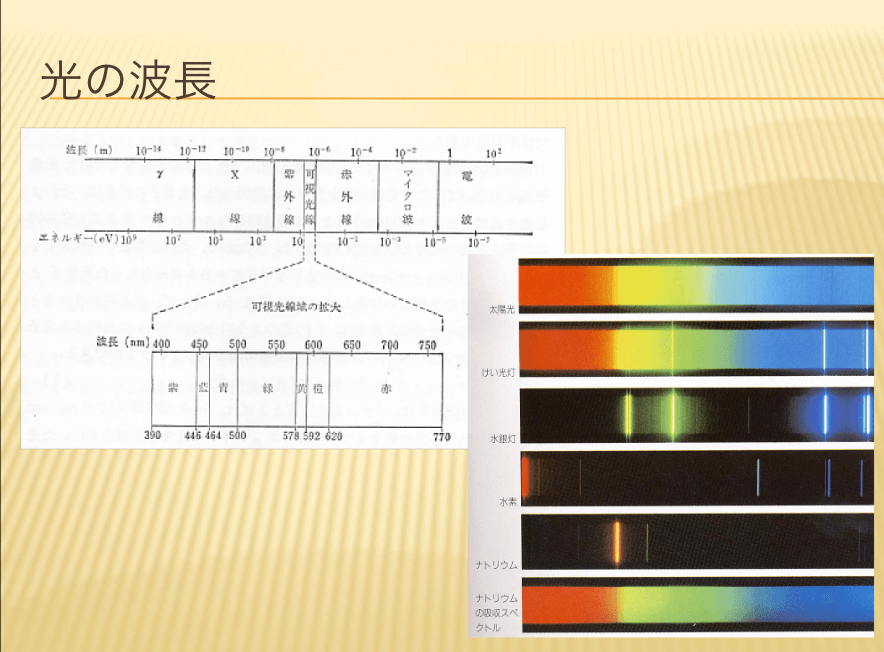
【光の波長】
光は粒子か波動かという論争がありますが、私の講義では基本的に、光は「波動」という立場でお話しします。けれど、現象を説明するために、粒子的に考えた方が理解しやすい場合があります。時には粒子的な考えで説明する場合もあります。
【ニュートンの実験(太陽光の分散)】
こちらは、ニュートンの有名な光学という本に書いてある、太陽光をプリズムで分けた時の実験の絵です。本人が描いたといわれています。
【フェルマーの原理】
光はどう進むのか、光線はどう進むのかと考えたときに、フェルマーという人はこのようにいいました。A点からB点に光が進む経路は、光が通る時間の最初になればよいです。つまり、最初の時間で伝わるような経路になればいいといったのです。
【屈折】
屈折の法則を今のフェルマーの定理で証明します。
【フェルマーの原理】
フェルマーの原理は、光が進む経路を表す非常に基本的な原理になっています。しかし、なぜこうなるのかは分かっていません。
しかし、力学の基本的な構成と、幾何光学の基本的な構成は非常に類似性があります。つまり、物理の基本的な概念から導けるものなのです。
【レンズのパワー(屈折力)】
パワー(屈折力)という値があります。それはレンズ焦点距離分の1になります。レンズの度数とも言います。単位はジオプターです。
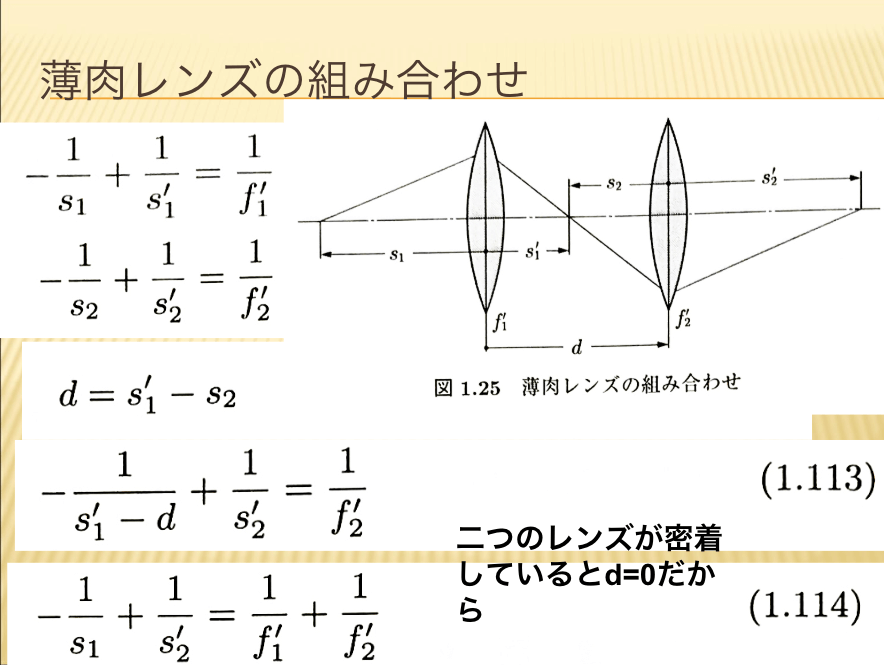
【薄肉レンズの組み合わせ】
今度は薄肉レンズが2枚の時、どうなるのかみてみましょう。第1の薄肉レンズでできる像が、今度第2の薄肉レンズの物体の位置になり、そこで像がどこにできるかという計算を行います。
【厚肉レンズ】
厚さを無視しないものが、厚肉レンズといわれています。かなり込み入った式になると予想されますが、見通しのよい量を定義すると、非常にすっきりした式を導くことができます。
幾何光学(2)
【光学系における距離の取り方、符号】
これから、複雑な光学系をどのような像ができるのか、光線がどんな風に進むのかということを、様々な場面に従って解析していきます。その際に、非常に重要なシステマティックに解析を進めるための取り決めをします。
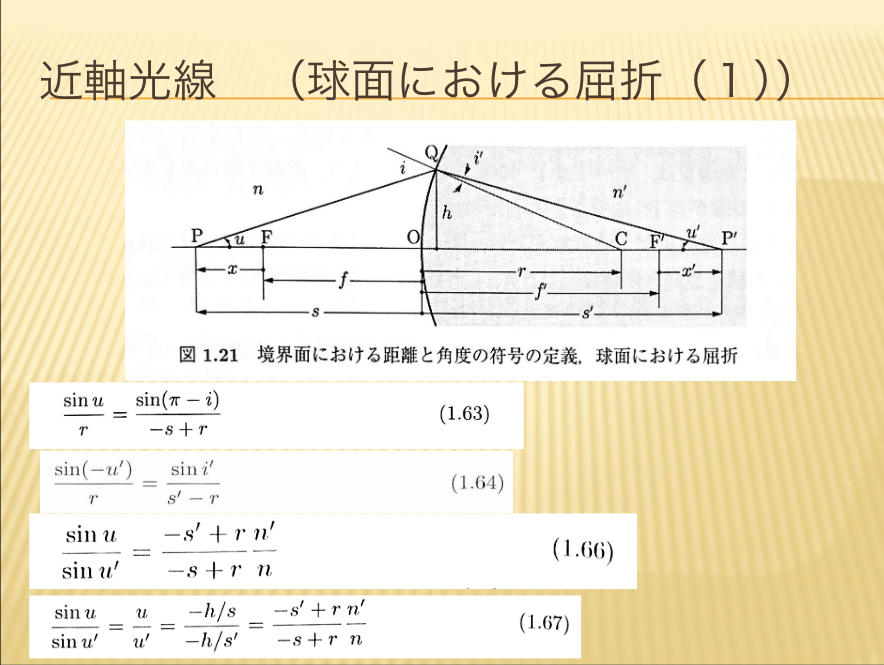
【近軸光線(球面における屈折(1))】
面の曲率半径r は負です。点 Pから発する光線と基準軸とのなす角をu,点 P’における光線と基準軸のなす角をu’とします。角度の測り方は、基準線(ここでは基準軸であり、屈折の場合には境界面に立てた垂線)から光線を見た最小の角度で反時計回りの方向を正とします。ここで、光線の高さを hとします。u,u’が十分に小さいときには, tan u= h/(-s), tan(ーu’) = h/s’ と書けます。
【球面における屈折(2)】
この式は、光線の角度に無関係に成立するので、点 Pからいろいろな角度で出射した光線束は、すべて点 P’に収束します。つまり、近軸光線のみを考えた場合には、点 Pの像が点 P’にできることがわかります。このように、光線束が 1点に収束するとき、点 P’は点 Pの実像(real image)といいます。一方、光線を逆向きに延長したとき、1点で交わる場合にはこれを虚像(imagenary image)といいます。光線逆進の原理から、点 P’から光路を逆進する光線束は、点 Pで像を結ぶことがわかります。物点 Pと像点 P’は互いに共役(conjugate)の関係にあるといいます。
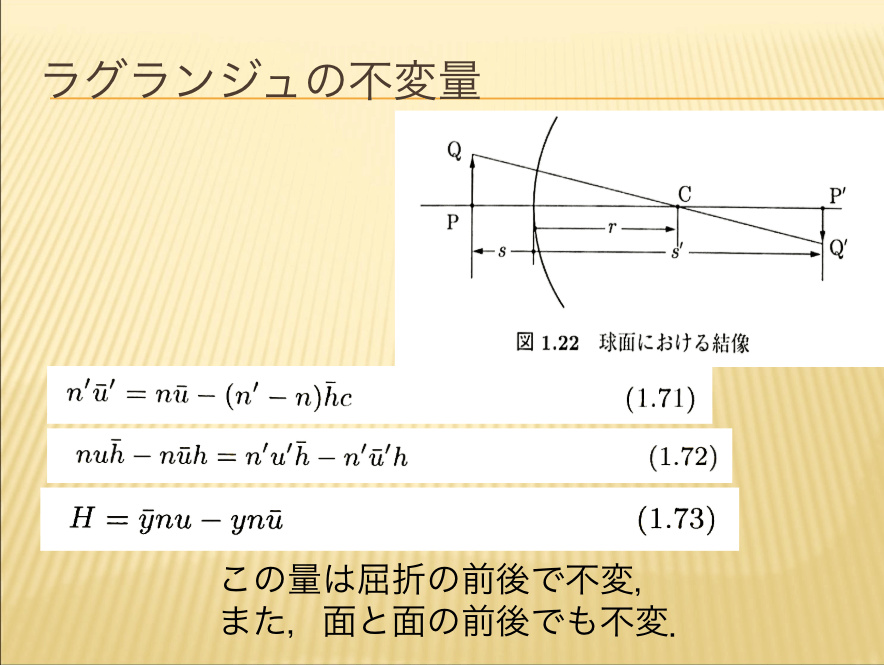
【ラグランジュの不変量】
この量は屈折の前後でも不変であり、これをラグランジュの不変量と呼びます。(Lagrangein-variant)と呼びます。またこれは、面と面の前後でも不変なのです。
【焦点距離】
焦点距離は物体が無限にあった時の、像の位置が焦点です。物点が無限遠にあると s=一∞で、入射光線は基準軸に平行になります。このときの像点の位置 s’=f’を後側焦点(focal point)F’といい、 f’を焦点距離(focal length)といいます。また、像点が無限遠にあるときの物点位置を前側焦点 Fといい、焦点距離はs=fです。計算してみましょう。
【ニュートンの式】
次に、焦点を原点として物点と像点までの距離を定義してみましょう。これをニュートンの結像式といいます。
【倍率(横倍率)】
倍率とは、物体の高さと像の高さの比です。計算してみましょう。
【倍率(縦倍率,角倍率)】
どのくらい光軸上で上下に伸び縮みするものが横倍率、縦が縦倍率といいます。
ヘルムホルツ・ラグランジェの不変量(Helmholtz-Lagrange invariant)とは、互いに共役な関係にある 2点間に成立する関係のことをいいます。
【球面における反射】
それから球面の反射した場合も考えると次のような関係になります。
ここで注意しなければならない点は、距離sとs’の符号、そして、屈折率です。
【薄肉レンズ(1)】
薄肉レンズとは先程の1の球面での屈折が2回あるのです。レンズの前と後ろの面に存在します。
【厚肉レンズ】
厚肉レンズ(普通のレンズ)の場合を考えてみましょう。考え方は、薄肉レンズの場合と同じように、物点、像点位置を定義します。
【主要点(主点,節点)】
主点もしくは主平面というものを考えると、非常に解析の見通しがよくなります。
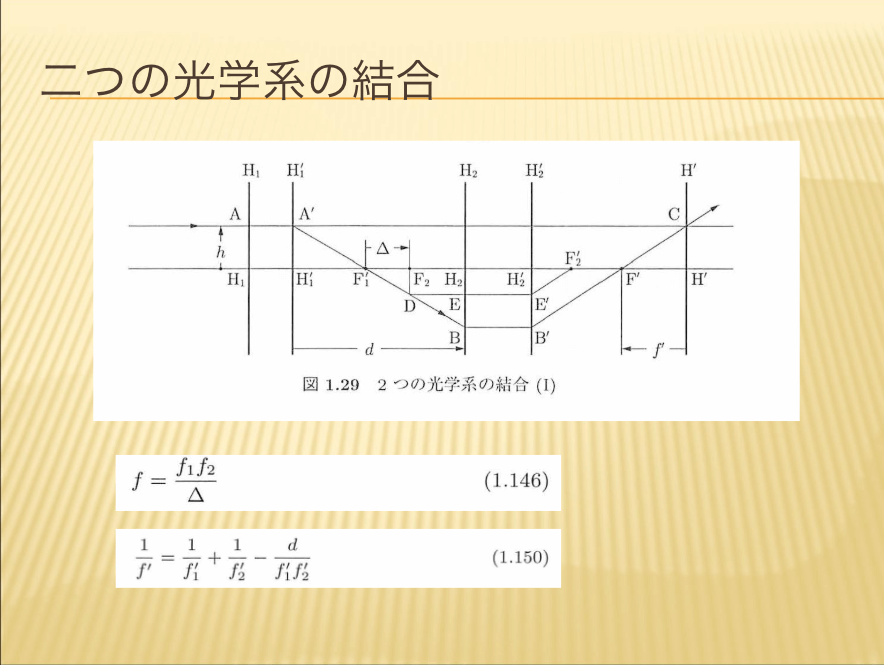
【二つの光学系の結合】
一つの光学系レンズではなく、一般化してみるとどんな複雑な光学系でも、その光学系全体では2つの平面があるということもいえます。だから、普通のカメラレンズが何枚か入っていたとすると、必ず一つのペアの主平面、前側主点と後ろ側主点が決まるで、そこから焦点距離を測ればよいのです。カメラレンズの一番後ろの面から、焦点距離を測っているわけじゃないということを注意してください。では、問題を解いてみましょう。
【アフォーカル光学系】
望遠鏡のような光学系では、非常に遠くにある物体の像を作るため、物体は非常に遠いところにあります。そのためほとんどの光線は、光軸に平行に入ってくるのです。望遠鏡の一番先端の対物レンズは、像を平行に出す光学系になっています。つまり、物体の位置も無限大になっているような、そのような光学系を誇る光学系をアフォーカル光学系といいます。
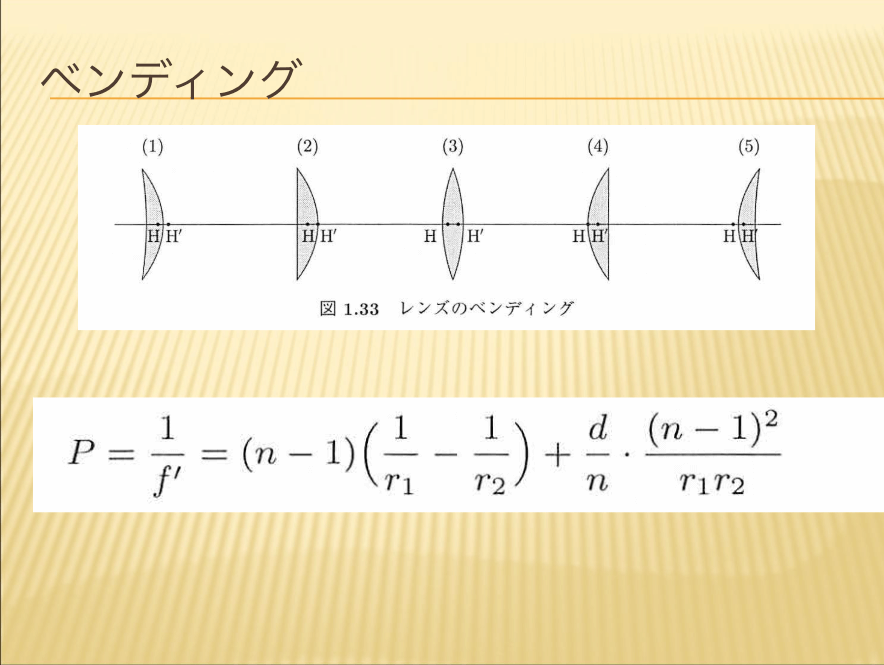
【ベンディング】
2つの球面の曲率半径の一方を変えても他方を適切に決めれば、単レンズの焦点距離を不変に保つことができます。これをベンデイング(bending)といいます。単レンズの主点位置は、ベンデイングの状態により変化します。 2つの主点位置がレンズの外側にある場合もあります。また、平凸レンズあるいは平凹レンズでは、一方の主点位置は、平面の境界面と反対側の境界面上に位置することがわかります。
【絞り】
絞り(stop)とは、光学系に入射する光来の太さを制限する関口(aperture)です。絞りには、目的の異なる二通りの使い方があります。すなわち,入射光量を制限する関口絞りと像の範囲を制限する視野絞りがあります。
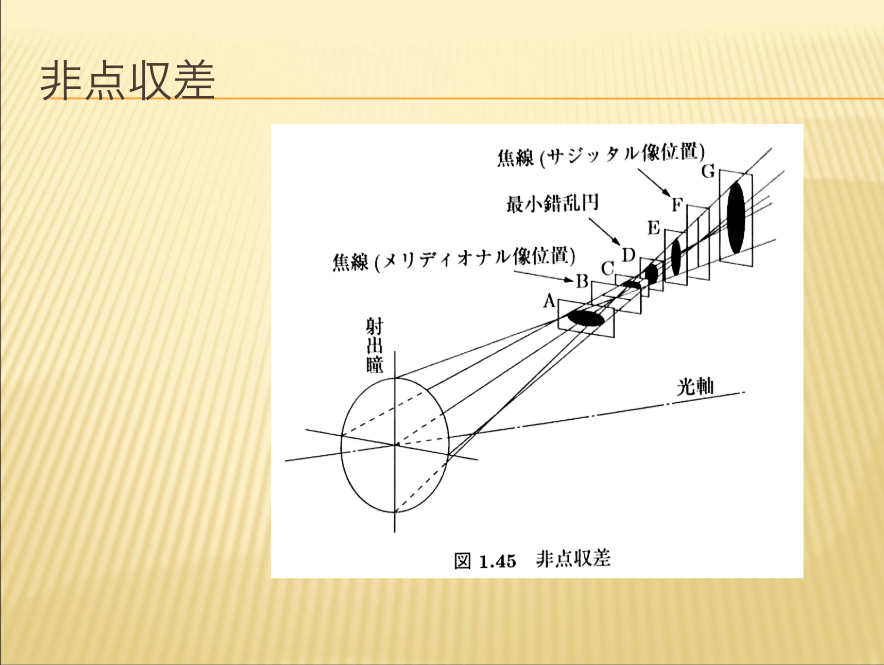
【非点収差】
今度は光学系に斜めから入ってくることを考えてみましょう。
光軸から外れた点物体からの光束がレンズに入射した後、1点に収束しないことがあります。これは光軸と主光線を含む面(これを子午断面(meridional plane)と呼びます)内の光線がつくる像点と、この面に垂直で主光線を含む面(これを球欠断面(sagittalplane)と呼びます)内の光線がつくる像点が異なるからです。このことを非点収差(astimatism)といいます。子午的(メリディオナル)光線がつくる像位置と球欠的(サジッタル)光線がつくる像位置の距離を非点隔差といい、非点隔差のほぼ中間に円形に近い小さな像(最小錯乱円という)ができます。非点収差は、光軸外の物体についてのみ発生します。非点収差が除かれたレンズをアナスティグマートといいます。
【像面湾曲】
非点収差があると、メリディオナル光線がつくる像面(メリディオナル像面)と、サジッタル光線がつくる像面(サジッタル像面)の 2つが存在し、その中間に実質的な像面が存在します。この像は必ずしも平面とはならず、湾曲しています。一般に、平面物体は、平面像面には結像されません。このような収差を、像面湾曲(curvature of field)といいます。
【歪曲】
球面収差、コマ収差、非点収差あるいは像面湾曲は像の鮮明度を低下させる収差です。これらの収差が低くが抑えられても、まだ、物体と像とを相似に結像することはできません。薄肉凸レンズの前側に絞りが置かれた場合には絞りに斜めに入射する光線はレンズの周辺を通りより多くの屈折を受け、矩形物体がたる形に歪むことになります。
【色収差】
光の波長が変わると屈折率も変化するので、収差も変化します。これが、色収差 (chro-matic aberration)です。色収差には、波長によって焦点距離が変化する軸上色収差と、波長によって結像倍率が変化することに起因する倍率色収差があります。
【アッべ数】
色収差を考えるうえで、光学ガラスの分散特性を 1つの数値にしておくと都合がよいです。
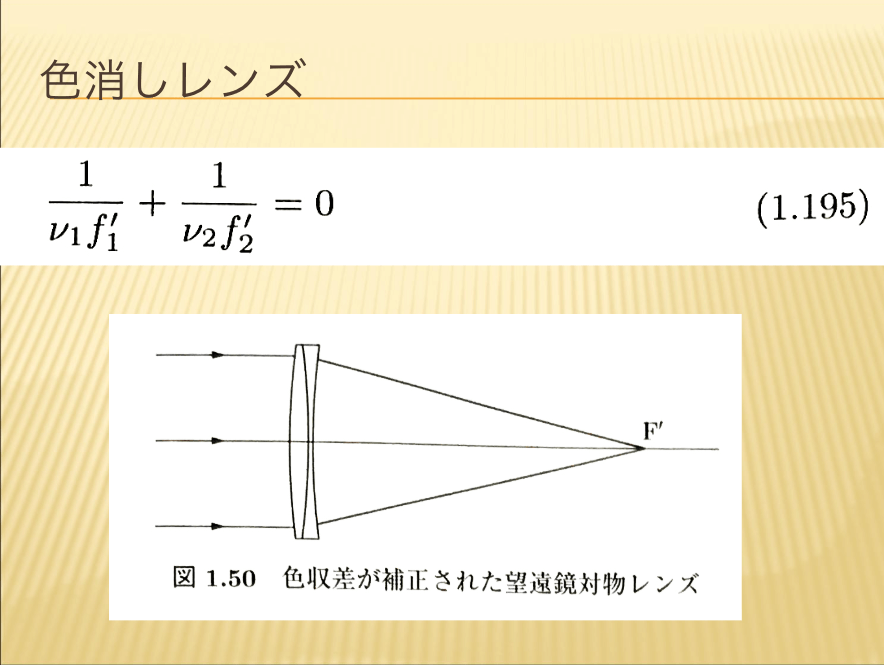
【色消しレンズ】
色収差を除いたレンズを色消しレンズ(achromatic lens)といいます。
【波面収差】(動画では「球面収差」となっていますが、正しくは「波面収差」です)
これまで考えてきた収差は、点物体から出た光線が理想像点に収束しない場合に、理想像点からの偏差として定義されてきた、幾何光学的な収差です。収差の記述法として、波面の概念による方法もあります。
【拡大鏡(ルーペ)】
薄肉凸レンズで物体を拡大して見る場合を考えてみましょう。正立虚像(erect imaginary image)を見ることになるので、レンズの前側焦点位置よりもレ ンズ側に物体Pを置く必要があります。
【顕微鏡】
極めて小さい物体を拡大して見る光学器械が、顕微鏡(microscope)です。顕微鏡対物レンズ(microscopic objective lens)によってできた拡大倒立実像を、接眼レンズでさらに拡大します。
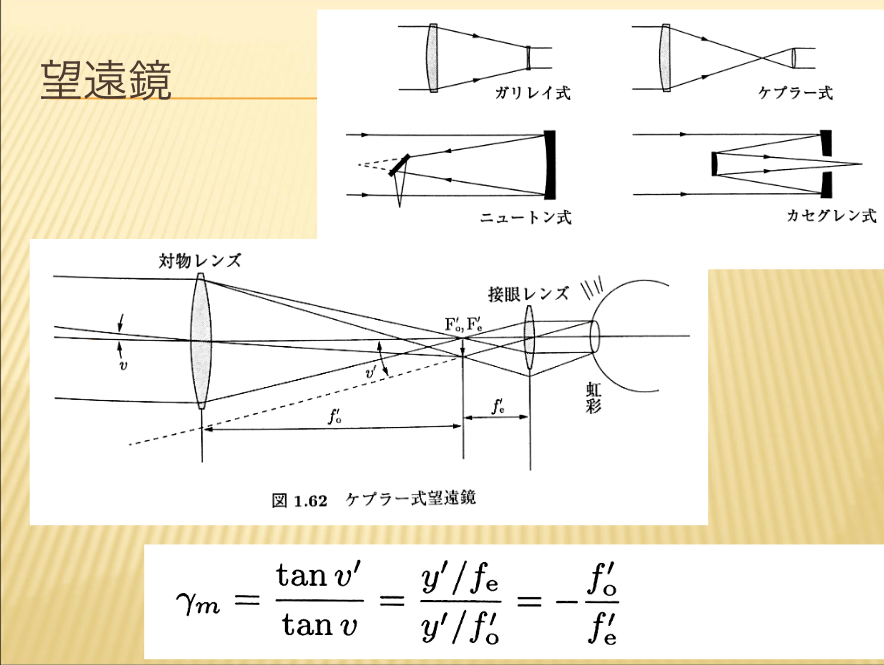
【望遠鏡】
遠方の物体を拡大して見るための光学器械が、望遠鏡(telescope)です。望遠鏡には、レンズを使う屈折望遠鏡と反射鏡を使う反射望遠鏡があります。屈折望遠鏡には、遠方から来る平行光を対物レンズで結像し、これを凸の接眼レンズで拡大するケプラ ー(Kepler)式と, 凹接眼レンズを用いるガリレイ(Galilei)式があります。
【近軸光線の追跡(行列表示)】
光学系の設計には、何枚ものレンズや反射鏡を組み合わせて、目的とする光学特性や性能(焦点距離、倍率、収差特性、分解能など)を実現する必要があります。これを光学設計といいます。光学設計では、まず、近軸光線で大まかな光学特性の評価を行い、次に、収差を考慮した光学特性の評価を行い、目的の特性を満たす、媒質の屈折率、境界面の曲率半径、面間隔などを最適化します。
【光線ベクトル】
光線を光軸に対する換算角度 U と高さ h を成分とするベクトルで表します。計算してみましょう。
【光学系行列】
一例として、単レンズを通過する場合の光線の変換を考えてみましょう。
【厚肉レンズ】
屈折率が n で、肉厚が t のレンズを考えてみましょう。
波動としての光
偏光
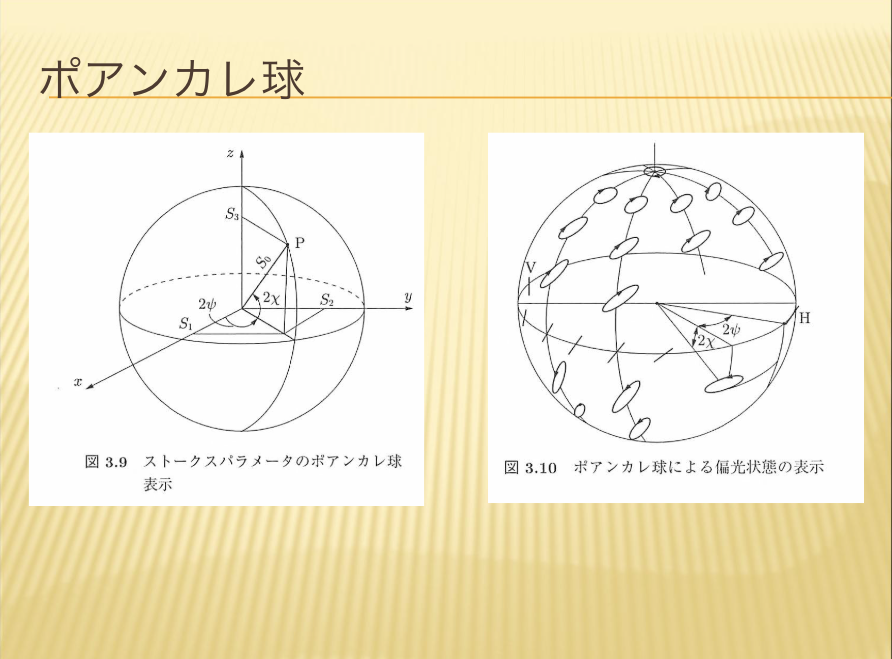
【ポアンカレ球】
4×4の行列で計算しようとしますが、さらに見通しが良くなる方法がないか、ということで考えられた方法が1つあります。
それがポアンカレ球というものを使う方法です。
【ジョーンズベクトル】
もう少し単純な場合を考える方法がジョーンズベクトルというものです。
ストークスパラメーターは、偏光してる光と偏光していない光を全て含めて表しています。測定可能な全ての偏光状態を表すことができますが、もう少し単純に偏光している成分を表わす方法として、EX成分とEY成分が分かればよいのです。これをスライドの式のように表すことができ、これジョーンズベクトルといいます。
【ジョーンズ行列】
偏光はジョーンズベクトルで表せるということが分かりました。今度はこのジョーンズベクトルを別の状態に変えるための行列、ミューラー行列と同じような議論ができるのです。
【波長板の回転】
波長板の回転の計算について考えていきましょう。
【直交直線偏光子】
まず最初に、水平方向に偏光成分を取り出す偏光板を置き、それから垂直方向に取り出す偏光板を設置すると、これはどんな光も全て通さな苦なります。さらにこの真ん中に直線偏光子を入れ、回転させると光は通るようになります。なぜそうなるのでしょう。計算をしてみましょう。
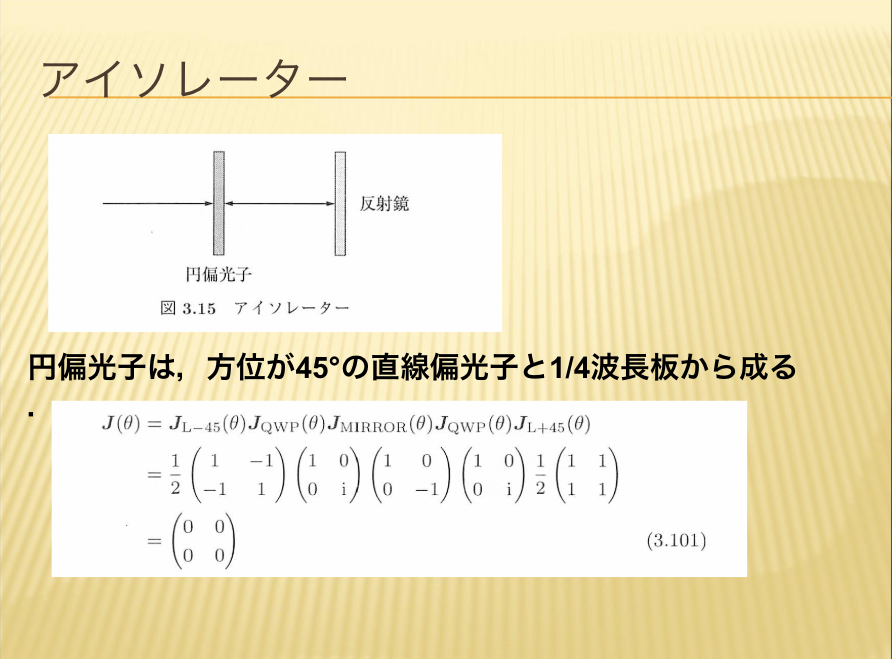
【アイソレーター】
最後に、興味深い例を紹介します。
レーザー光は、光の共振器になっています。その共振器から出たレーザー光がもとに戻ってくると、共振の条件が狂い、共振が非常に不安定になることがあります。特に半導体レーザーはそれを大変嫌います。例えば光ファイバーは、半導体レーザーから出てきた光を、光ファイバーに当て入れるときに、反射して元に戻る成分があります。また、光ファイバーの途中で様々なものを置いた時には、半導体レーザーの出力が変化し、非常に不安定になるということがよくあります。
【質疑応答】
Q1, 無偏光のストークスベクトルS0=1他は0 は物理的には理解できるが、電場のEx Eyの表示から導出する方法は何ですか?
Q2, 1000の無偏光な光をポアンカレ球にプロットする際は、どこにプロットすればいいのでしょうか?
Q3, 先生の以前のご研究で微分干渉顕微鏡のプリズムをジョーンズベクトルで解析する、があったと思います。ノマルスキープリズム等をジョーンズマトリックスで書く場合どのように考えると理解しやすいですか?
干渉
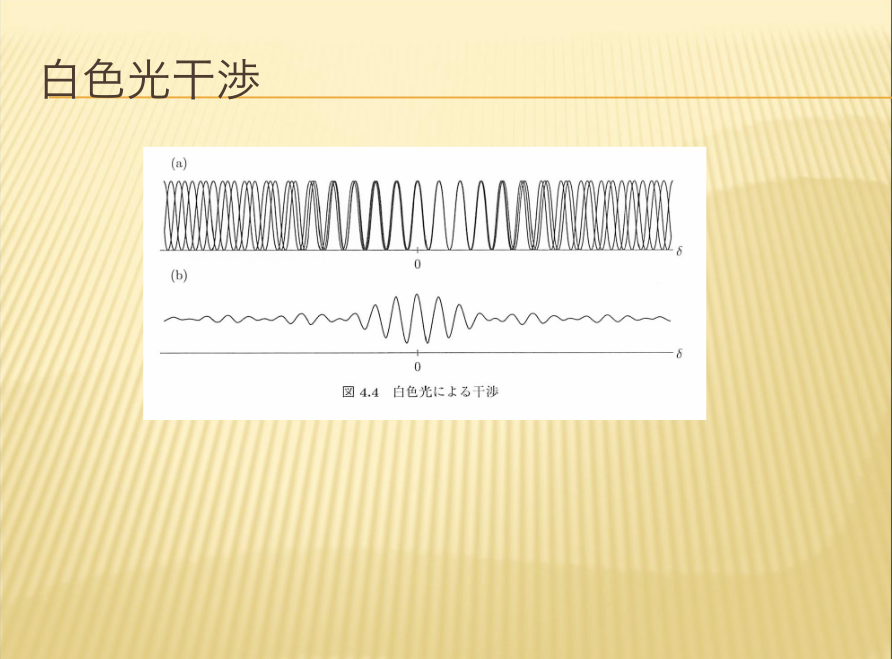
【白色光干渉】
ある共通の非常に小さな光源から出てきた光を、2つに分けて重ねると干渉縞が出てきます。それが光が波動であるということを証明しているのです。さらに詳しく解説いたします。
【干渉縞の鮮明度】
干渉縞は、理想では強度が0から1まで終始的に変化します。実際には、光源の波長がある程度広がったり、光源が1点ではなく、光源自身が広がり、波長が広がるなどの様々な変化がみられます。すると干渉縞の明るさが0から1まで終始的に変化せず、平均値の周りを上下変動するのです。
【時間的可干渉性】
先ほどお話したように、光源が今までの計算では、理想的には、オメガは0ならオメガ0という、非常に決まった周波数、波長の光に対しての理論でした。しかし実際にはそうではなく、波長はある広がりを持っており、光る場所もある広がりを持っています。点から出てくるだけではなく、たくさんの原子から光が出てきます。空間的に広がることによって干渉縞の鮮明度が変わるのです。
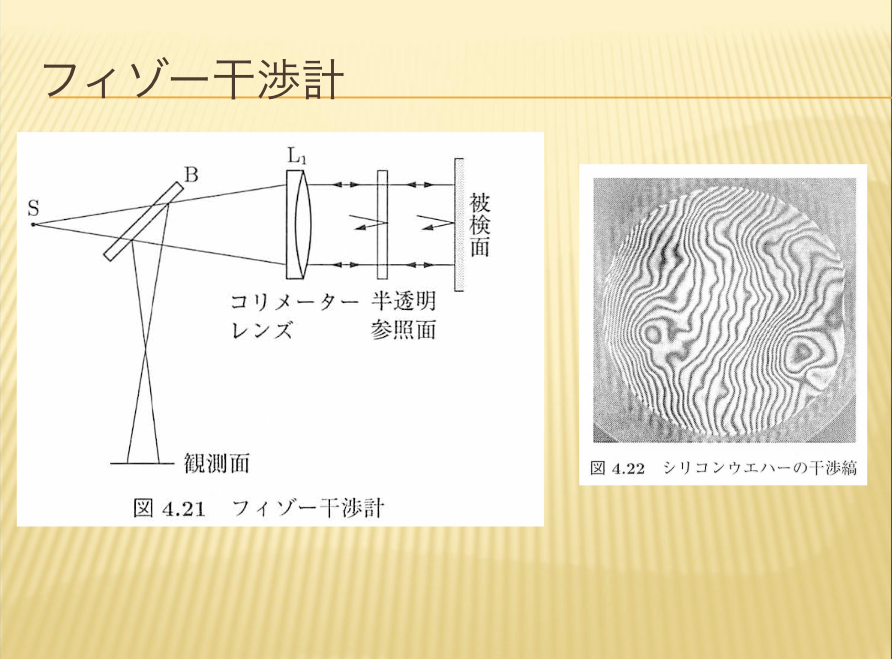
【フィゾー干渉計】
フィゾー干渉計は日常的に、非常に多く使われています。ほとんどの市販の干渉計はこの構成になっています。
原理的には、トワイマン・グリーン干渉計と同じですが、より詳しく解説いたします。
回析
【質疑応答】
Q,スカラー波で議論していたと思うのですが、それがベクトル波になった時に
主に変わるのはどのあたりになるのでしょうか?
A,偏光の影響です。
回答について詳しく解説していきます。
フーリエ光学
【空間周波数フィルタリング】【周波数制限フィルター】
結像で幾何光学との対話を取るために、非常に重要な概念です。
ここからは情報処理に関して、周波数を変化させることにより別の像を作るという話をしていきます。
【マッチトフィルター】
マッチトフィルターについての解説です。
【結合フーリエ変換相関器】
相関関数の計算の際に、合成を取ることができます。
そのことについて解説していきます。
【ホログラフィ】
3次元的な物体があり、ここからレーザー光で証明し、解析されてきた光がホログラムです。物体の記録方法であるホログラフィについて解説していきます。
【ホログラムの種類】
物体光と参照光が干渉するようなコヒーレントな光で実現すれば、どんな配置でも波面は記録することはできます。物体から来た波面を記録することができます。いろんな種類があります。
【計算機ホログラム】
今まではホログラムをつくるための実際に物を置き、そのものを証明して解析されてきた波を、参照波と干渉させてホログラムを作ってきたわけですが、そのプロセスを全部計算機の中でやることができます。
【ディジタルホログラフィ】
実際のホログラムを、実際のものと参照波を当ててできる干渉縞。そのホログラムをイメージセンサーや、画像入力装置で読み取るとディジタル的なホログラムができます。
それを今度は数値的に検出されたイメージセンサーで、検出されたホログラムに架空の光を当てた時のフレネル回折を計算すると、その像が見えます。
これをディジタルホログラフィーと言います。
【ホログラフィの応用】
回折光学素子といった、応用のお話をしていきます。
【ホログラフィ干渉】
ホログラフィックのもとの3次元物体から来る位相分布というか、形状分布をそのまま記録することができます。
多くの物体がほんの少しずれたり、変形したりしますが、その変形前の像と変形後の像を2つ同時に再生すると、その間の干渉縞が見えます。これををホログラフィー干渉といいます。
【質疑応答】
Q1、レンズのフーリエ変換の作用を確認する際に、線分の長さから位相のズレを計算したと思うのですが、その計算で追えなかったところがあったため詳しく解説していただきたいです。
Q2、前回セミナー回折に関して、角スペクトルのZ軸の依存性についての質問です。
物質と光
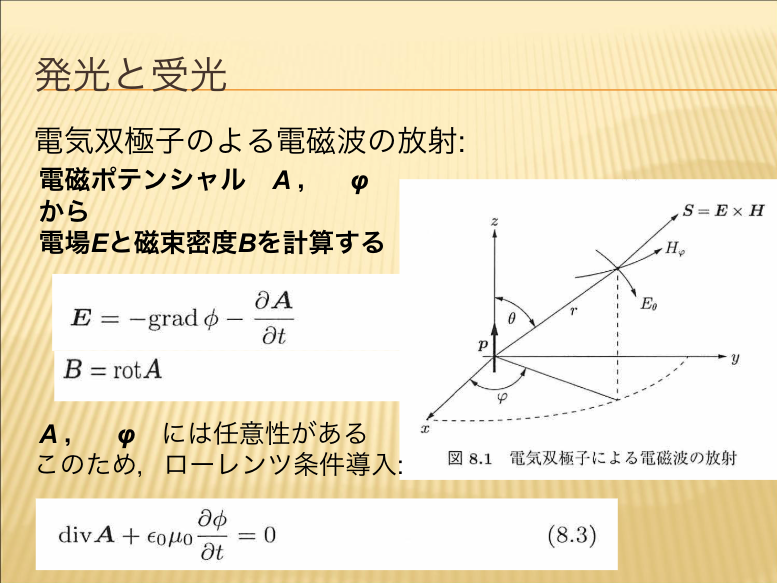
【発光と受光】
電子が振動することによって、電波を出すということが発光です。物質に光が当たる交流の電界・磁界の振動がおこると、それによって物質の中の電子が励起され、電気の流れが生じます。あるいは、抵抗の変化が生じることで光がきたかどうか、また光の量の大きさが分かります。これが受光です。
【双極子からの放射】
電子双極子モーメントの式、また電子双極子の振動により発生される電流、その電流によるポテンシャルを表す式の解説です。
【電気双極子の振動はZ方向とする】
電子双極子の振動をA方向のみとした場合、ベクトルポテンシャルは「双極子からの放射」で登場した式と同じように表すことができます。それらを極座標に書き換えた場合、どうなるのかという解説です。
【双極子から十分離れたところでは】
通常は電子が振動して、それを観測するのは、電子の大きさに比べて非常に離れたところで観測するだけになります。そこでの式はどうなるのか。また、放射される電界と磁界によるエネルギーはポインティングベクトルで表すことができます。その式についての解説です。
【双極子による電磁波の放射】
電子双極子が、Z方向に振動することによって放出されるエネルギーの式を、XYZ形態で書いた場合の解説です。
【黒体からの光放射(プランクの式)】
物質が温められた時、その熱の効果により電子も振動します。
その際、振動方向がでたらめになりどのようなエネルギーの光が放射されるのかということが問題になります。
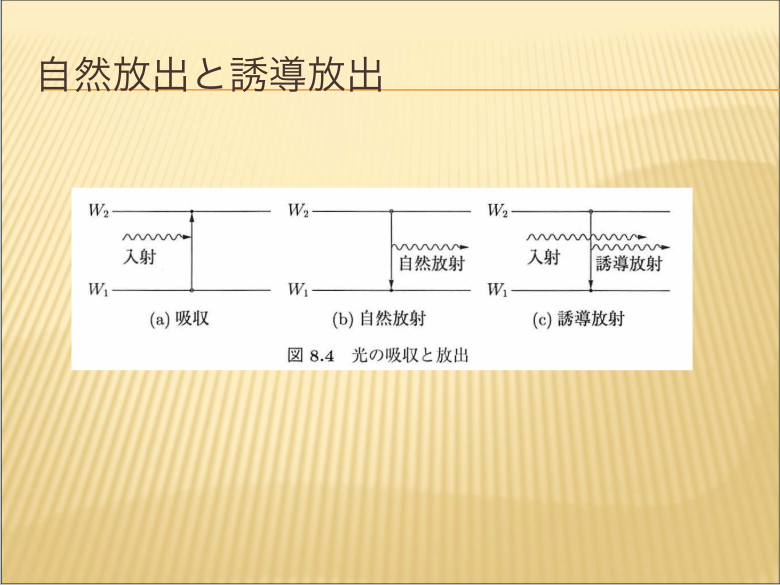
【自然放出と誘導放出】
普通の物質は量子重力によると低いエネルギー状態にあり、何度かの過程で高い状態になったとすると、光を発して安定する低い状態になります。そして、光を吸収すると低いエネルギーから高いエネルギーになります。そのモデルについての解説です。
【蛍光とLED】
高いエネルギー状態に、ちょうど条件を満たすような光を入射する状態を作るやり方の一つの解説です。
【レーザー】
反転分布をつくるための共振器の解説です。
【半導体励起固体レーザー(DPSS)】
反転分布をうまく作るために、いろいろな機構がありますが、半導体レーザーによる光ではどうなるのかという解説です。
【ファイバーレーザー】
最近ファイバーの材料として使用されている、エルビウムという原子をドープした光ファイバーについての解説です。
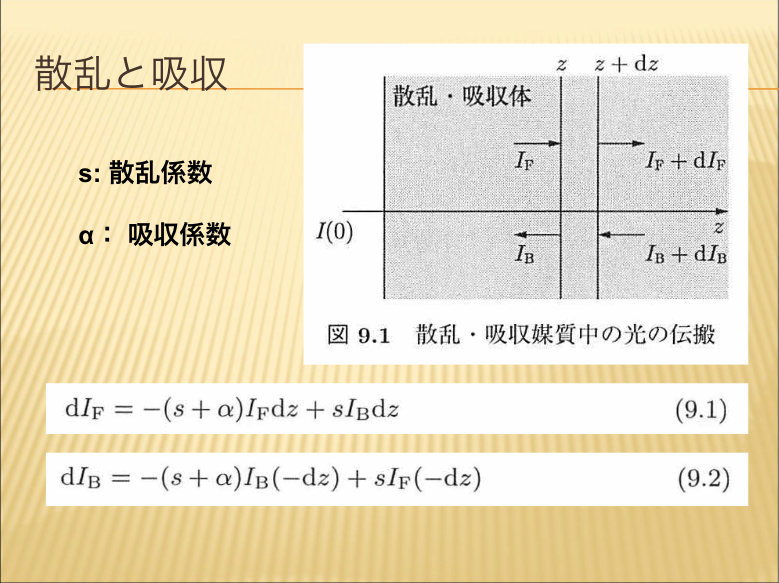
【散乱と吸収】
物質の中を光が伝わる際に、散乱や吸収という現象がおきます。
その現象を利用すると、さまざまな面白い現象を説明することができます。
【ランバート・ベールの法則】
「逆方向に進む光束が無視できる場合」「ランバートの法則」
逆方向に進む光束が無視できる場合の式と、ランバートの法則を表す式の解説です。
「散乱が無視できて、吸収がその濃度に比例する時」「ベールの法則」
ベールの法則についての解説です。
【クベルカ・ムンクの式】
入ってきた時の物質の光強度と、反射してきた光強度の比をとった場合の式と、分厚い層の場合の式についての解説です。
【微粒子や媒質による散乱】
非常に微細な粒子や媒質のところでは、正反射せず、光がいろんな方向に、散乱されます。そういった現象についての解説です。
【散乱断面積】
散乱断面積とはどういうものかについての解説です。
【散乱式】
「レイリー散乱」「ミー散乱」「屈折による散乱」「サイズパラメーター」を説明する際に使用する式についての解説です。
【ミー散乱】
非常に小さな粒子に光が入ると、いろいろな方向に散乱されます。
その散乱光と照明された光が複雑に干渉し、複雑なパターンで放射されます。その計算が非常に面倒なのですが、今回は簡単に説明します。
【火星の夕日は青い!】
実は火星の夕日は青いです。これはミー散乱の影響で、火星は地球と比べて大気が薄いことや、重力が非常に小さいということがポイントになってきます。
【表面による反射】
「鏡面反射をするか、表面反射をするかは表面の凹凸の振幅によって決まる。」ということについての解説です。
被等方媒質中の光
【偏光子(グラントムソンプリズム)】
グラントムソンプリズムは材料が方解石です。一軸性の負の結晶である方解石を用いた例についてお話ししていきます。
【位相板】
位相板の厚さを上手く調整すると、2分の1波長板や8分の1波長板ができます。
【複像プリズム】
進む方向が違う性質をうまく使って、異なる偏光を違う方向に進ませるようなものを複像プリズムといいます。
これにはウォーラストンプリズムやロションプリズム、セルナモンプリズムなどがあります。
【光学活性(OPTICAL ACTIVITY)】
これまでは非等方性の媒質についてのお話しでしたが、それに少し関連するものとして光学活性があります。それについて解説していきます。
【二色性(DICHROISM)】
右回りの特別な偏光に対して吸収がある、例えば垂直方向の偏光と水平方向の変更について吸収率が違う場合を二色性といいます。
【液晶】
液晶というものは通常の結晶と実体の中間のようなもので、分子が規則的に並ぶと通常の結晶ですが、それが音の条件によって
並び方が変わります。そのようなものを液晶といいます。
測光と測色 ガウスビームの伝播
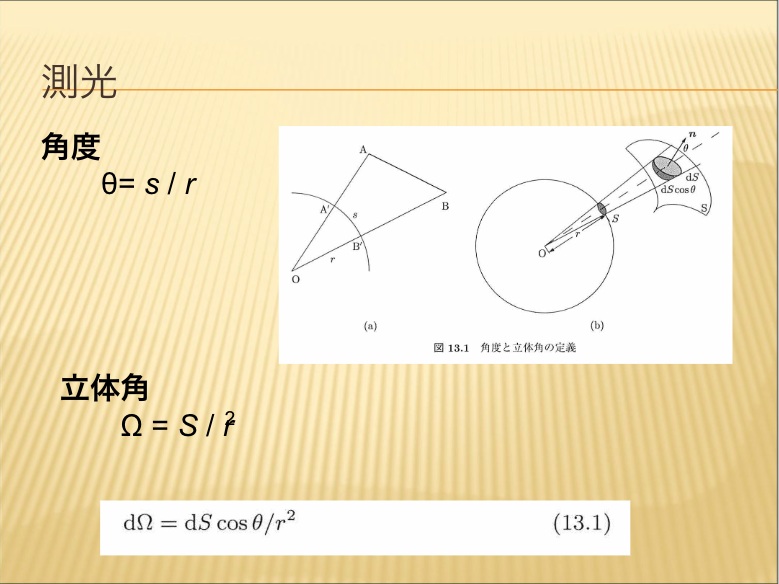
【測光】
ここからタイトルにもある測光と測色についてのお話に入っていきます。
測光の話に入る前に、覚えておくべきである「角度」と「立体角」についての説明をします。
【立体角】
前トピックで解説した立体角を、極座標形で書くとどうなるのかについて説明します。
【放射量と測光量】
単位面積に当たった光のエネルギーの量や、どのくらい明るく見えるのかということを定量的に解析しなければいけません。このことを「測光」といいます。
実際のエネルギーの大きさで明るさを評価するのか、人間の目で見た時の明るさで評価するのとでは少し違ってきます。
物理的に定義したエネルギーから来る量を「放射量」といい、人間の目の感度を考慮したものを「測光量」といいます。
【質疑応答】
Q,人によって見え方が異なることには、目の色が関係しているのでしょうか?それとも網膜が関係しているのでしょうか?
A,私は原因がよくわかっていないので、答えにはなっていないのですが、昔のテレビを例を挙げると、ヨーロッパの人が日本に来てテレビを見ると画面が青いということがありました。逆に我々がヨーロッパに行くと、街全体が赤っぽく見えるような気がします。何となくですが、日本人は緑っぽいものが好きで、ヨーロッパやアメリカの人たちは黄色っぽいものや赤色が好きなだということを聞いたことがあります。
レーザー・光学の動画学習サービス OptiVideo
豊富なレーザー・光学の動画コンテンツが定額で見放題で、他では聞けない有名な先生の講義が視聴可能です。
労働安全衛生法やJIS C6802を網羅したレーザー安全の講義内容を発信。
使用者、管理者にマストな、あらゆる危険に備える知識を「OptiVideo」で学べます。
また、月1回以上のWebセミナー講習が無料で聴講可能です。